题目内容
3、已知点I是锐角三角形ABC的内心,A1,B1,C1分别是点I关于BC,CA,AB的对称点,若点B在△A1B1C1的外接圆上,则∠ABC等于( )
分析:首先根据题目说明勾勒如图所示.通过图很容易知道IA1=IB1=IC1=2r(r为△ABC的内切圆半径).在Rt△IBD中,利用直角三角形性质,斜边是直角边的2倍,则该直角边所对的角为30°.即可知∠IBD=30°.同理,∠IBA=30°,于是∠ABC=60°.问题得解.
解答: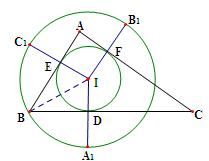 解:∵IA1=IB1=IC1=2r(r为△ABC的内切圆半径)
解:∵IA1=IB1=IC1=2r(r为△ABC的内切圆半径)
∴I点同时是△A1B1C1的外接圆的圆心
设IA1与BC的交点为D,则IB=IA1=2ID
∴∠IBD=30°
同理,∠IBA=30°,于是∠ABC=60°
故选C.
 解:∵IA1=IB1=IC1=2r(r为△ABC的内切圆半径)
解:∵IA1=IB1=IC1=2r(r为△ABC的内切圆半径)∴I点同时是△A1B1C1的外接圆的圆心
设IA1与BC的交点为D,则IB=IA1=2ID
∴∠IBD=30°
同理,∠IBA=30°,于是∠ABC=60°
故选C.
点评:本题考查三角形的内切圆与内心、三角形外接圆与外心、直角三角形的性质.解决本题的关键是首先根据题意画出几何图形,再将求角大小转化为在直角三角形中求角的大小.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 OC,
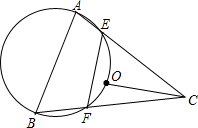
OC,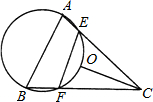 如图,已知点O是锐角三角形ABC的外心,过A、B、O三点的圆交于AC、BC于E、F,且EF=OC.
如图,已知点O是锐角三角形ABC的外心,过A、B、O三点的圆交于AC、BC于E、F,且EF=OC.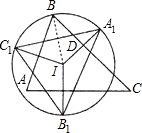 已知点I是锐角三角形ABC的内心,A1、B1、C1分别是点I关于边BC,CA,AB的对称点,若点B在△A1B1C1的外接圆上,则∠ABC等于
已知点I是锐角三角形ABC的内心,A1、B1、C1分别是点I关于边BC,CA,AB的对称点,若点B在△A1B1C1的外接圆上,则∠ABC等于