Question

【题目】已知：如图，在平行四边形ABCD中，AE是BC边上的高，将△ABE沿BC方向平移，使点E与点C重合，得△GFC．

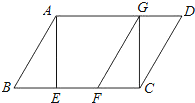
（1）求证：BE=DG；

（2）若∠B=60°，当AB与BC满足什么数量关系时，四边形ABFG是菱形？证明你的结论．

Answer 1

【答案】（1）见解析；（2）四边形ABFG是菱形，见解析

【解析】

试题分析：（1）根据平移的性质，可得：BE=FC，再证明Rt△ABE≌Rt△CDG可得：BE=DG；

（2）要使四边形ABFG是菱形，须使AB=BF；根据条件找到满足AB=BF的AB与BC满足的数量关系即可．

（1）证明：∵四边形ABCD是平行四边形，

∴AB=CD．

∵AE是BC边上的高，且CG是由AE沿BC方向平移而成．

∴CG⊥AD．

∴∠AEB=∠CGD=90°．

∵AE=CG，

∴Rt△ABE≌Rt△CDG（HL）．

∴BE=DG；

（2）解：当BC=AB时，四边形ABFG是菱形．

证明：∵AB∥GF，AG∥BF，

∴四边形ABFG是平行四边形．

∵Rt△ABE中，∠B=60°，

∴∠BAE=30°，

∵BC=AB

∴BE=CF

∴EF=AB

∴AB=BF

∴四边形ABFG是菱形，