��Ŀ����
����Ŀ����֪�����ߵı���ʽ��y=ax2+��1��a��x+1��2a��aΪ������0�ij���������������������aΪ��ֵʼ�վ�������A�Ͷ���B��AΪx���ϵĵ㣬BΪ��һ�����ڵĵ㣮
��1����д��A��B��������꣺A���� ����0����B���� ������ ������
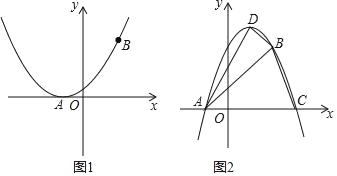
��2����ͼ1������������x��ֻ��һ��������ʱ����a��ֵ��
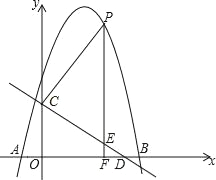
��3����ͼ2����a��0ʱ�������������߶�����D����x�����һ����Ϊ��C���ҵ�A��B��C��D��û����������غϣ�
�١�ABC�ܷ���ֱ�������Σ�Ϊʲô��
����ʹ�á�ABD��ֱ�������Σ��������a��ֵ�������1��a��ֵ���ɣ�
���𰸡���1����1��2��3����2��a=![]() ����3����a=��
����3����a=��![]() ����a=��1��
����a=��1��
��������
��1��y=ax2+��1-a��x+1-2a=a��x2-x-2��+x+1������x2-x-2��=0ʱ������aΪ��ֵʼ�վ�������A�Ͷ���B��������⣻
��2������������x��ֻ��һ��������ʱ����=0��������⣻
��3����A��-1��0������C��x��0����AB���ڵ�ֱ�ߵ�k1ֵΪ1��BC���ڵ�ֱ�ߵ�k2ֵΪ��![]() =3a����k1k2=-1������⣻���裺��ABD=90�����裺D��m��n��������Τ�ﶨ���ã�m2=-
=3a����k1k2=-1������⣻���裺��ABD=90�����裺D��m��n��������Τ�ﶨ���ã�m2=-![]() ����m=-
����m=-![]() ����y=ax2+��1-a��x+1-2a֪��m=
����y=ax2+��1-a��x+1-2a֪��m=![]() ������-
������-![]() =
=![]() ��������⣮
��������⣮
�⣺��1��y=ax2+��1��a��x+1��2a=a��x2��x��2��+x+1��
����x2��x��2��=0ʱ������aΪ��ֵʼ�վ�������A�Ͷ���B��
��x=��1��2����A����1��0����B��2��3����
�ʣ����ǩ�1��2��3��
��2������������x��ֻ��һ��������ʱ����=0��
������1��a��2��2a��1��2a��=0����ã�a=![]() ��
��
��3����A����1��0������C��x��0����
��Τ�ﶨ������1x=![]() ����C��
����C��![]() ��0����
��0����
AB���ڵ�ֱ�ߵ�k1ֵΪ1��
BC���ڵ�ֱ�ߵ�k2ֵΪ��![]() =3a��
=3a��
��k1k2=��1ʱ��AB��BC����ã�a=��![]() ��
��
���裺��ABD=90�㣬
��ֱ��BD����ֱ�߷��̵�k=��1����ֱ�߷���Ϊ��y=��x+5��
��ֱ��BD���ڵķ�������κ��������ã�
ax2+��2��a��x����4+2a��=0��
�裺D��m��n������B��2��3��
��Τ�ﶨ���ã�m2=��![]() ����m=��
����m=��![]() ��
��
��y=ax2+��1��a��x+1��2a֪��m=![]() ��
��
������![]() =
=![]() ��
��
��ã�a=��1��

 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�