题目内容
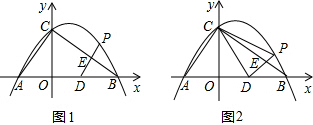 已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上,点D的坐标为(2,0).
已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上,点D的坐标为(2,0).(1)填空:线段OA的长度为
1
1
,OB的长度为4
4
,经过点A、B、C的抛物线的关系式为y=-
x2+
x+2
| 1 |
| 2 |
| 3 |
| 2 |
y=-
x2+
x+2
;| 1 |
| 2 |
| 3 |
| 2 |
(2)点P(m,n)是该抛物线上的一个动点(其中m>0,n>0),连接DP交BC于点E,当△BDE是等腰三角形时,请直接写出此时点E的坐标.
(3)连接CD、CP,△CDP是否有最大面积?若有,求出△CDP的最大面积和此时点P的坐标;若没有,请说明理由.
分析:(1)由Rt△ABC中,CO⊥AB可证△AOC∽△COB,由相似比得OC2=OA•OB,设OA的长为x,则OB=5-x,代入可求OA,OB的长,确定A,B,C三点坐标,求抛物线解析式;
(2)根据△BDE为等腰三角形,分为DE=EB,EB=BD,DE=BD三种情况,分别求E点坐标;
(3)将求△CDP的面积问题转化,如图4,连接OP,根据S△CDP=S四边形CODP-S△COD=S△COP+S△ODP-S△COD,表示△CDP的面积;再利用二次函数的性质求出△CDP的最大面积和此时点P的坐标.
(2)根据△BDE为等腰三角形,分为DE=EB,EB=BD,DE=BD三种情况,分别求E点坐标;
(3)将求△CDP的面积问题转化,如图4,连接OP,根据S△CDP=S四边形CODP-S△COD=S△COP+S△ODP-S△COD,表示△CDP的面积;再利用二次函数的性质求出△CDP的最大面积和此时点P的坐标.
解答:(1)解:设OA的长为x,则OB=5-x;
∵OC=2,AB=5,∠BOC=∠AOC=90°,∠OAC=∠OCB;
∴△AOC∽△COB,
∴OC2=OA•OB
∴22=x(5-x),
解得:x1=1,x2=4,
∵OA<OB,∴OA=1,OB=4;
∴点A、B、C的坐标分别是:A(-1,0),B(4,0),C(0,2);
方法一:设经过点A、B、C的抛物线的关系式为:y=ax2+bx+2,
将A、B、C三点的坐标代入得:
解得:
,
所以这个二次函数的表达式为:y=-
x2+
x+2,
方法二:设过点A、B、C的抛物线的关系式为:y=a(x+1)(x-4),
将C点的坐标代入得:a=-
,
所以这个二次函数的表达式为:y=-
x2+
x+2,
 故答案为:1,4,y=-
故答案为:1,4,y=-
x2+
x+2;
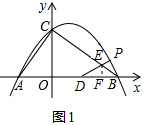
(2)解:如图1,当DE=EB时,过点E作EF⊥BD于点F,
∵BO=4,OD=2,∴BD=2,
∵DE=BE,EF⊥BD,
∴DF=FB=
BD=1,
∴OF=OD+DF=3,
∵EF⊥BO,CO⊥BO,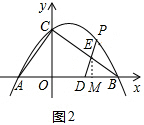
∴EF∥CO,
∴△COB∽△EFB,
∴
=
,
∴
=
,
∴EF=
,
故E点坐标为:(3,
),
如图2,当EB=BD时,过点E作EM⊥BO于点M,
∵CO=2,BO=4,
∴BC=2
,
∵点D的坐标为(2,0),
∴BD=BE=4-2=2,
∵EM∥CO,
∴△COB∽△EMB,
∴
=
,
∴
=
,
∴EM=
,
∵
=
=
,
∴BM=
,
∴MO=4-
,
∴故E点坐标为:(4-
,
),
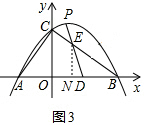
如图3,当DE=BD时,过点E作EN⊥BO于点N,
设E点横坐标为x,则ND=2-x,故BN=4-x,
∵
=
,
∴EN=
(4-x),
∴在Rt△END中,
EN2+ND2=ED2,
即[
(4-x)]2+(2-x)2=22,
解得:x=
,
∴EN=
(4-x)=
,
故点E的坐标是:(
,
),
故当△BDE是等腰三角形时,点E的坐标分别是:(3,
),(
,
),(4-
,
).
(3)解:如图4,连接OP,
∵P点坐标为:(m,n),
∴P到CO距离为m,P到x轴距离为n,
S△CDP=S四边形CODP-S△COD=S△COP+S△ODP-S△COD,
=
×2m+
×2n-
×2×2=m+n-2
=-
m2+
m,
=-
(m-
)2+
,
∴当m=
时,n=
,此时△CDP的面积最大.此时P点的坐标为(
,
),
S△CDP的最大值是
.
∵OC=2,AB=5,∠BOC=∠AOC=90°,∠OAC=∠OCB;
∴△AOC∽△COB,
∴OC2=OA•OB
∴22=x(5-x),
解得:x1=1,x2=4,
∵OA<OB,∴OA=1,OB=4;
∴点A、B、C的坐标分别是:A(-1,0),B(4,0),C(0,2);
方法一:设经过点A、B、C的抛物线的关系式为:y=ax2+bx+2,
将A、B、C三点的坐标代入得:
|
解得:
|
所以这个二次函数的表达式为:y=-
| 1 |
| 2 |
| 3 |
| 2 |
方法二:设过点A、B、C的抛物线的关系式为:y=a(x+1)(x-4),
将C点的坐标代入得:a=-
| 1 |
| 2 |
所以这个二次函数的表达式为:y=-
| 1 |
| 2 |
| 3 |
| 2 |
 故答案为:1,4,y=-
故答案为:1,4,y=-| 1 |
| 2 |
| 3 |
| 2 |
(2)解:如图1,当DE=EB时,过点E作EF⊥BD于点F,
∵BO=4,OD=2,∴BD=2,
∵DE=BE,EF⊥BD,
∴DF=FB=
| 1 |
| 2 |
∴OF=OD+DF=3,
∵EF⊥BO,CO⊥BO,

∴EF∥CO,
∴△COB∽△EFB,
∴
| CO |
| EF |
| BO |
| FB |
∴
| 2 |
| EF |
| 4 |
| 1 |
∴EF=
| 1 |
| 2 |
故E点坐标为:(3,
| 1 |
| 2 |
如图2,当EB=BD时,过点E作EM⊥BO于点M,
∵CO=2,BO=4,
∴BC=2
| 5 |
∵点D的坐标为(2,0),
∴BD=BE=4-2=2,
∵EM∥CO,
∴△COB∽△EMB,
∴
| CO |
| EM |
| BC |
| EB |
∴
| 2 |
| EM |
2
| ||
| 2 |
∴EM=
2
| ||
| 5 |
∵
| CO |
| BO |
| EM |
| MB |
| 1 |
| 2 |
∴BM=
4
| ||
| 5 |

∴MO=4-
4
| ||
| 5 |
∴故E点坐标为:(4-
4
| ||
| 5 |
2
| ||
| 5 |
如图3,当DE=BD时,过点E作EN⊥BO于点N,
设E点横坐标为x,则ND=2-x,故BN=4-x,
∵
| CO |
| BO |
| 1 |
| 2 |
∴EN=
| 1 |
| 2 |
∴在Rt△END中,
EN2+ND2=ED2,
即[
| 1 |
| 2 |
解得:x=
| 4 |
| 5 |
∴EN=
| 1 |
| 2 |
| 8 |
| 5 |
故点E的坐标是:(
| 4 |
| 5 |
| 8 |
| 5 |
故当△BDE是等腰三角形时,点E的坐标分别是:(3,
| 1 |
| 2 |
| 4 |
| 5 |
| 8 |
| 5 |
4
| ||
| 5 |
2
| ||
| 5 |
(3)解:如图4,连接OP,
∵P点坐标为:(m,n),

∴P到CO距离为m,P到x轴距离为n,
S△CDP=S四边形CODP-S△COD=S△COP+S△ODP-S△COD,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 5 |
| 2 |
=-
| 1 |
| 2 |
| 5 |
| 2 |
| 25 |
| 8 |
∴当m=
| 5 |
| 2 |
| 21 |
| 8 |
| 5 |
| 2 |
| 21 |
| 8 |
S△CDP的最大值是
| 25 |
| 8 |
点评:本题考查了二次函数的综合运用.关键是根据直角三角形中斜边上的高分得的两个三角形相似,以及根据等腰三角形的性质求E点坐标,利用作辅助线的方法表示△CDP的面积,由二次函数的性质求三角形面积的最大值.

练习册系列答案
相关题目
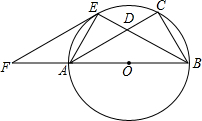 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.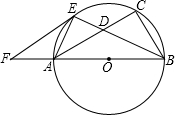 ∥AC交BA的延长线于F.
∥AC交BA的延长线于F.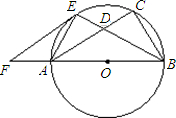 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交