题目内容
【题目】数形结合是数学解题中的一种重要思想，利用数轴可以将数与形完美结合．一般地，数轴上表示数m和数n的两点之间的距离等于|m﹣n|，如：数轴上表示4和1的两点之间的距离是|4﹣1|＝3；表示﹣3和2两点之间的距离是|﹣3﹣2|＝5．
根据以上材料，结合数轴与绝对值的知识回答下列问题：
（1）将数﹣5，﹣
，0，2.5在数轴上表示出来．
（2）若数轴上表示数a的点位于﹣3与2之间，那么|a+3|+|a﹣2|的值是多少？
（3）若A是数轴上的一个点，它表示数a，则|a+5|+|a﹣3|的最小值是多少？当a取多少时|a+5|+|a﹣1|+|a﹣3|有最小值？最小值是多少？
【答案】（1）详见解析；（2）5；（3）8;a=1;8．
【解析】
（1）在数轴上标示出﹣5，﹣
，0，2.5即可求解；（2）由图可得﹣3＜a＜2，然后根据绝对值的意义对|a+3|+|a-2|进行化简，即可求解；（3）根据|a+5|+|a-1|+|a-3|表示A点到-5，1，3三点的距离的和确定当﹣5＜a＜3时，|a+5|+|a﹣3|的值最小，然后根据绝对值的意义进行化简．
解：（1）如图所示：
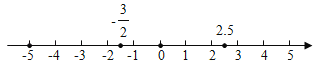
（2）①∵﹣3＜a＜2，
∴|a+3|+|a﹣2|＝a+3+2-a＝5；
（3）∵|a+5|+|a-1|+|a-3|表示A点到-5，1，3三点的距离的和
∴当﹣5＜a＜3时，|a+5|+|a﹣3|的值最小，且为a+5+3-a=8,是定值，
∴a＝1时，|a﹣1|最小为0，
∴a＝1时，|a+5|+|a﹣1|+|a﹣3|的最小值等于8．
练习册系列答案
相关题目
