题目内容
如图,在△ABC中,AC = BC,AB = 8,CD⊥AB,垂足为点D.M为边AB上任意一点,点N在射线CB上(点N与点C不重合),且MC = MN.设AM = x.

(1)如果CD = 3,AM = CM,求AM的长;
(2)如果CD = 3,点N在边BC上.设CN = y,求y与x的函数解析式,并写出函数的定义域;
(3)如果∠ACB = 90°,NE⊥AB,垂足为点E.当点M在边AB上移动时,试判断线段ME的长是否会改变?说明你的理由.

(1)如果CD = 3,AM = CM,求AM的长;
(2)如果CD = 3,点N在边BC上.设CN = y,求y与x的函数解析式,并写出函数的定义域;
(3)如果∠ACB = 90°,NE⊥AB,垂足为点E.当点M在边AB上移动时,试判断线段ME的长是否会改变?说明你的理由.

(1) (2)
(2) ,
, (3)线段ME的长不变,理由见解析
(3)线段ME的长不变,理由见解析
 (2)
(2) ,
, (3)线段ME的长不变,理由见解析
(3)线段ME的长不变,理由见解析解:(1)∵ AC = BC,∴ ∠A =∠B.
∵ AC = BC,CD⊥AB,∴ .……………………(1分)
.……………………(1分)
由勾股定理,得 .………………(1分)
.………………(1分)
∵ AM = CM,∴ ∠A =∠ACM.
即得 ∠ACM =∠B.
∴ △ACM∽△ABC.…………………………………………………(1分)
∴ .∴
.∴  .即得
.即得  .………………(1分)
.………………(1分)
(2)过点M作MF⊥BC,垂足为点F.
由 AM = x,得 BM =" 8" –x.
∵ MF⊥BC,CD⊥AB,
∴∠MFB =∠ADC = 90°.
又∵ ∠A =∠B,∴ △MBF∽△ACD.……………………………(2分)
∴ .即得
.即得  .
.
∴ .
.
∴ .…………………………(1分)
.…………………………(1分)
∵ MC = MN,MF⊥BC,
∴ .
.
即得 .……………………………………………………(1分)
.……………………………………………………(1分)
定义域为 .………………………………………………(1分)
.………………………………………………(1分)
(3)当点M在边AB上移动时,线段ME的长不变,ME = 4.…………(1分)
由点N在射线CB上,可知点N在边BC上或点N在边CB的延长线上.
(ⅰ)如果点N在边BC上,可知点M在线段AD上.
∵ AC = BC,∠ACB = 90°,∴ ∠A =∠B = 45°.
又∵ AC = BC,CD⊥AB,AB = 8,
∴ CD = BD = 4.
即得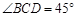 .
.
∵ MC = MN,∴ ∠MCN =∠MNC.
∵ ∠MCN =∠MCD +∠BCD,∠MNC =∠B +∠BMN,
∴ ∠MCD =∠NME.
又∵ CD⊥AB,NE⊥AB,∴ ∠CDM =∠MEN = 90°.
∴ △MCD≌△MNE(A.A.S).
∴ ME = CD = 4.……………………………………………………(2分)
(ⅱ)如果点N在边CB的延长线上,可知点M在线段BD上,且点E在边AB的延长线上.
于是,由 ∠ABC =∠MNC +∠BMN = 45°,
∠BCD =∠MCD +∠MCN = 45°,
∠MCN =∠MNC,
得 ∠MCD =∠BMN.
再由 MC = MN,∠CDM =∠MEN = 90°,
得 △MCD≌△MNE(A.A.S).
∴ ME = CD = 4.……………………………………………………(2分)
∴ 由(ⅰ)、(ⅱ)可知,当点M在边AB上移动时,线段ME的长不变,ME = 4.
(1)由勾股定理求得AC=5,然后利用相似三角形的相似比求出 ;
;
(2)证明△MBF∽△ACD,可得 ;
;
(3)注意点N在射线CB上,应该包括两种情况:点N在边BC上或点N在边CB的延长线上.
∵ AC = BC,CD⊥AB,∴
 .……………………(1分)
.……………………(1分)由勾股定理,得
 .………………(1分)
.………………(1分)∵ AM = CM,∴ ∠A =∠ACM.
即得 ∠ACM =∠B.
∴ △ACM∽△ABC.…………………………………………………(1分)
∴
 .∴
.∴  .即得
.即得  .………………(1分)
.………………(1分)(2)过点M作MF⊥BC,垂足为点F.
由 AM = x,得 BM =" 8" –x.
∵ MF⊥BC,CD⊥AB,
∴∠MFB =∠ADC = 90°.
又∵ ∠A =∠B,∴ △MBF∽△ACD.……………………………(2分)
∴
 .即得
.即得  .
.∴
 .
.∴
 .…………………………(1分)
.…………………………(1分)∵ MC = MN,MF⊥BC,
∴
 .
.即得
 .……………………………………………………(1分)
.……………………………………………………(1分)定义域为
 .………………………………………………(1分)
.………………………………………………(1分)(3)当点M在边AB上移动时,线段ME的长不变,ME = 4.…………(1分)
由点N在射线CB上,可知点N在边BC上或点N在边CB的延长线上.
(ⅰ)如果点N在边BC上,可知点M在线段AD上.
∵ AC = BC,∠ACB = 90°,∴ ∠A =∠B = 45°.
又∵ AC = BC,CD⊥AB,AB = 8,
∴ CD = BD = 4.
即得
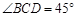 .
.∵ MC = MN,∴ ∠MCN =∠MNC.
∵ ∠MCN =∠MCD +∠BCD,∠MNC =∠B +∠BMN,
∴ ∠MCD =∠NME.
又∵ CD⊥AB,NE⊥AB,∴ ∠CDM =∠MEN = 90°.
∴ △MCD≌△MNE(A.A.S).
∴ ME = CD = 4.……………………………………………………(2分)
(ⅱ)如果点N在边CB的延长线上,可知点M在线段BD上,且点E在边AB的延长线上.
于是,由 ∠ABC =∠MNC +∠BMN = 45°,
∠BCD =∠MCD +∠MCN = 45°,
∠MCN =∠MNC,
得 ∠MCD =∠BMN.
再由 MC = MN,∠CDM =∠MEN = 90°,
得 △MCD≌△MNE(A.A.S).
∴ ME = CD = 4.……………………………………………………(2分)
∴ 由(ⅰ)、(ⅱ)可知,当点M在边AB上移动时,线段ME的长不变,ME = 4.
(1)由勾股定理求得AC=5,然后利用相似三角形的相似比求出
 ;
;(2)证明△MBF∽△ACD,可得
 ;
;(3)注意点N在射线CB上,应该包括两种情况:点N在边BC上或点N在边CB的延长线上.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 为
为 ,运动时间为
,运动时间为 ,则下列图形能大致地刻画
,则下列图形能大致地刻画
 、
、 两地相距10千米,甲班从
两地相距10千米,甲班从 小时,甲、乙两班离
小时,甲、乙两班离 千米、
千米、 千米,
千米,
 (
( )的图象不经过
)的图象不经过 与时间
与时间 之间函数关系的是
之间函数关系的是