Question

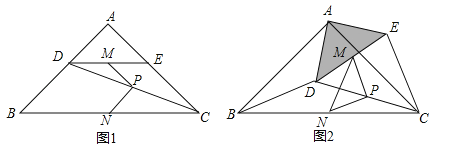
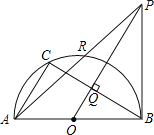
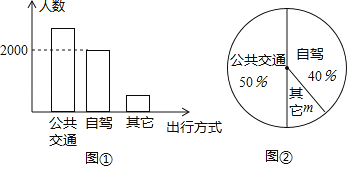
【题目】如图，△ABC是圆内接等腰三角形，其中AB=AC，点P在上运动（点P与点A在弦BC的两侧），连结PA，PB，PC，设∠BAC=α，=y，小明为探究y随α的变化情况，经历了如下过程

（1）若点P在弧BC的中点处，α=60°时，y的值是______．

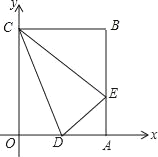
（2）小明探究α变化获得了一部分数据，请你填写表格中空缺的数据．在如图2平面直角坐标系中以表中各组对应值为点的坐标进行描点，并画出函数图象：

α	…	30°	60°	90°	120°	150°	170°	…
y	．．	0.52			1.73	1.93	1.99	…

（3）从图象可知，y随着α的变化情况是______；y的取值范围是______．

Answer 1

【答案】(1)1；(2)图象见解析；(3)随增大而增大，.

【解析】

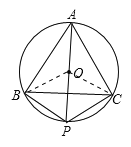
（1）连OB，OC，由△ABC是圆内接等腰三角形及α＝60°可知△ABC是⊙O的内接正三角形，由点P是弧BC的中点，根据垂径定理的推论得到AP为⊙O的直径，易得△OBP和△OPC都是等边三角形，于是得到结论；

（2）当α＝60°时，由(1)可知y=1；当α＝90°时，使三角形ACP绕A点旋转使得AC与AB重合；求出P、B、P’共线即可得出答案；

（3）观察图像可知y随着α增大而增大，并可看出的取值范围.

解：(1) 解：（1）连OB，OC，如图

∵△ABC是圆内接等腰三角形，α＝60°，

∴△ABC是⊙O的内接正三角形，

∵点P是弧BC的中点，△ABC是⊙O的内接正三角形，

∴AP为⊙O的直径，

∴∠BPO=∠ACB，∠APC=∠ABC，

∵△ABC是⊙O的内接正三角形，

∴∠ACB=∠ABC=60°，

∴∠BPO=∠APC=60°，

∴△OBP和△OPC都是等边三角形，

∴PB=PC=OP=OA，

∴PB+PC=PA，

则.

(2) 当α＝60°时，由(1)可知y=1；

当α＝90°时

使三角形ACP绕A点旋转使得AC与AB重合，如图

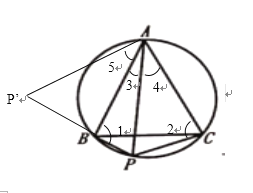
∵∠4=∠5,

∵∠3+∠4=90°，

∴∠3+∠5=90°，

又∵∠1+∠2=180°，

∴P、B、P’共线，

∵△APP’为直角三角形且AP=AP’，

∴=== ≈1.41

	...	30°	60°	90°	120°	150°	170°	...
	...	0.52	1	1.41	1.73	1.93	1.99	...

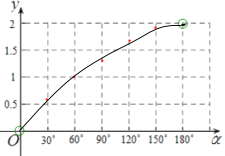
(3)由图象可知：随增大而增大，的取值范围是：．