题目内容
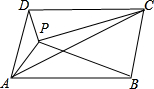 如图,已知P为平行四边形ABCD内一点,且S△PAB=5,S△PAD=2,则S△PAC等于( )
如图,已知P为平行四边形ABCD内一点,且S△PAB=5,S△PAD=2,则S△PAC等于( )| A、2 | B、3 | C、4 | D、5 |
分析:假设P点到AB的距离是h1,假设P点到DC的距离是h2,根据三角形的面积公式求出△PAB和△PDC的面积和,推出S△ADC=S△PAB+S△PDC=5+S△PDC和S△PAC=S△ADC-S△PDC-S△PAD,代入即可求出答案.
解答:解:∵四边形ABCD是平行四边形,
∴AB=DC,
假设P点到AB的距离是h1,假设P点到DC的距离是h2,
∴S△PAB=
AB•h1,S△PDC=
DC•h2,
∴S△PAB+S△PDC=
(AB•h1+DC•h2)=
DC•(h1+h2),
∵h1+h2正好是AB到DC的距离,
∴S△PAB+S△PDC=
S平行四边形ABCD=S△ABC=S△ADC,
即S△ADC=S△PAB+S△PDC=5+S△PDC,
而S△PAC=S△ADC-S△PDC-S△PAD,
∴S△PAC=5-2=3,
故选B.
∴AB=DC,
假设P点到AB的距离是h1,假设P点到DC的距离是h2,
∴S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△PAB+S△PDC=
| 1 |
| 2 |
| 1 |
| 2 |
∵h1+h2正好是AB到DC的距离,
∴S△PAB+S△PDC=
| 1 |
| 2 |
即S△ADC=S△PAB+S△PDC=5+S△PDC,
而S△PAC=S△ADC-S△PDC-S△PAD,
∴S△PAC=5-2=3,
故选B.
点评:本题主要考查对平行四边形的性质,三角形的面积等知识点的理解和掌握,能根据性质推出S△ADC=S△PAB+S△PDC=5+S△PDC,和S△PAC=S△ADC-S△PDC-S△PAD是解此题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目

 如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0)、
如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0)、 19、如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE把它分成的四部分的面积分别为S1S2S3S4,下面结论:
19、如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE把它分成的四部分的面积分别为S1S2S3S4,下面结论: 如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(1,0),B(6,0)和C(0,4 )三个点.
如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(1,0),B(6,0)和C(0,4 )三个点.