题目内容
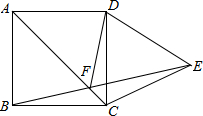 如图,以正方形 ABCD的一边向形外作等边三角形CDE,AC与BE交于F,则图中与∠AFD(包括∠AFD)相等的角的个数有( )
如图,以正方形 ABCD的一边向形外作等边三角形CDE,AC与BE交于F,则图中与∠AFD(包括∠AFD)相等的角的个数有( )分析:由正方形及等边三角形的边长相等,且DD为两图形的公共边,得到AD=AB=CD=AD=CE=DE,且正方形的四个角都为直角,等边三角形的三内角都为60°,且由正方形的对角线平分一组对角,得到∠BAF=∠DAF,利用SAS可证明三角形ABF与三角形ADF全等,从而得到∠AFB=∠AFD,然后由∠BCD为直角,∠DCE为60°的角求出∠BCE的度数,根据BC=EC,求出∠CBE的度数,由三角形的外角性质得到∠AFB为60°,∠AFB=∠AFD=60°,根据平角定义得到∠DFE也为60°,再利用对顶角相等得到∠CFE也为60°,最后加上等边三角形的三内角都为60°,得到所有与∠AFD(包括∠AFD)相等的角的个数即可.
解答:解:∵四边形ABCD是正方形,三角形DCE为等边三角形,
∴AB=BC=CD=AD=DE=CE,∠BCD=90°,∠BAF=∠DAF=45°,∠DCE=∠DEC=∠CDE=60°,
在△ABF与△ADF中,
,
∴△ABF≌△ADF(SAS),
∴∠AFD=∠AFB,
∵CB=CE,∴∠CBE=∠CEB,
∵∠BCE=∠BCD+∠DCE=90°+60°=150°,
∴∠CBE=15°,
∵∠ACB=45°,
∴∠AFB=∠ACB+∠CBE=60°,
∴∠AFD=∠AFB=60°,
∴∠EFD=60°,且∠AFB=∠EFC=60°(对顶角相等),
则图中与∠AFD(包括∠AFD)相等的角有:
∠DCE,∠DEC,∠CDE,∠AFD,∠DFE,∠AFB,∠EFC,共7个.
故选C
∴AB=BC=CD=AD=DE=CE,∠BCD=90°,∠BAF=∠DAF=45°,∠DCE=∠DEC=∠CDE=60°,
在△ABF与△ADF中,
|
∴△ABF≌△ADF(SAS),
∴∠AFD=∠AFB,
∵CB=CE,∴∠CBE=∠CEB,
∵∠BCE=∠BCD+∠DCE=90°+60°=150°,
∴∠CBE=15°,
∵∠ACB=45°,
∴∠AFB=∠ACB+∠CBE=60°,
∴∠AFD=∠AFB=60°,
∴∠EFD=60°,且∠AFB=∠EFC=60°(对顶角相等),
则图中与∠AFD(包括∠AFD)相等的角有:
∠DCE,∠DEC,∠CDE,∠AFD,∠DFE,∠AFB,∠EFC,共7个.
故选C
点评:此题考查了正方形的性质,等边三角形的性质,全等三角形的判定与性质,外角性质,以及对顶角的性质,借助图形,灵活运用性质求出∠AFD的度数是解本题的关键.本题还要注意答案要找全,不能漏解.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
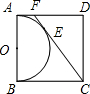 如图,以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点E,交AD边于点F,则
如图,以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点E,交AD边于点F,则
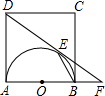 如图,以正方形ABCD的AB边为直径,在正方形内部作半圆,圆心为O,DF切半圆于点E,交AB的延长线于点F,BF=4.
如图,以正方形ABCD的AB边为直径,在正方形内部作半圆,圆心为O,DF切半圆于点E,交AB的延长线于点F,BF=4.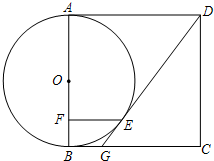 BF,作直线DE交BC于点G.若正方形的边长为10,EF=4.
BF,作直线DE交BC于点G.若正方形的边长为10,EF=4.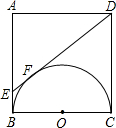 如图,以正方形ABCD的边BC为直径作半圆O,过点D作直线切半圆于点F,交AB边于点E,求△ADE和直角梯形EBCD周长之比.
如图,以正方形ABCD的边BC为直径作半圆O,过点D作直线切半圆于点F,交AB边于点E,求△ADE和直角梯形EBCD周长之比.