题目内容
已知直线y=| 1 |
| 2 |
(1)写出A,B两点的坐标(用含m的代数式表示),并求tanA的值;
(2)如果AC=4
| 5 |
分析:(1)令x=0以及y=0求出A,B的坐标.然后可求出tanA.
(2)已知△ABO是直角三角形,求出AB的值.证明△ACO∽△ABO,利用线段比求出m值.
(2)已知△ABO是直角三角形,求出AB的值.证明△ACO∽△ABO,利用线段比求出m值.
解答:解:(1)当x=0时,y=m,∴A(0,m);
当y=0时x=-2m,∴B(-2m,0).
tanA=
=
=2.
(2)在Rt△ABO中,OA=m,OB=2m,
∴AB=
m,
∵△ACO∽△AOB,
∴OA2=AC•AB,
m2=4
×
m,
∴m1=20,m2=0(不符合题意,舍去).
∴m的值为20.
当y=0时x=-2m,∴B(-2m,0).
tanA=
| OB |
| OA |
| 2m |
| m |
(2)在Rt△ABO中,OA=m,OB=2m,
∴AB=
| 5 |
∵△ACO∽△AOB,
∴OA2=AC•AB,
m2=4
| 5 |
| 5 |
∴m1=20,m2=0(不符合题意,舍去).
∴m的值为20.
点评:本题考查的是三角函数的有关知识,相似三角形的判定以及一次函数的综合题,难度中等.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 已知直线
已知直线 E两点,与x轴交于B、C两点,且B点坐标为(1,0).
E两点,与x轴交于B、C两点,且B点坐标为(1,0).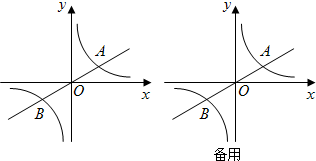
 (2013•梧州模拟)如图,已知直线y=
(2013•梧州模拟)如图,已知直线y=