Question

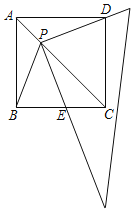
【题目】如图，一直角三角形的直角顶点P在边长为1的正方形ABCD对角线AC上运动（点P与A、C两点不重合）且它的一条直角边始终经过点D，另一直角边与射线BC交于点E．

（1）当点E在BC边上时，

①求证：△PBC≌△PDC；

②判断△PBE的形状，并说明理由；

（2）设AP＝x，△PBE的面积为y．

①求出y关于x的函数关系式，并写出x的取值范围；

②当x取何值时，y取得最大值，并求出这个最大值．

Answer 1

【答案】（1）①见解析；②△PBE是等腰三角形；（2）①；当x＝时，y最大值＝．

【解析】

（1）①根据SAS证明两三角形全等；

②由△PBC≌△PDC得∠PBC＝∠PDC，由∠BCD＝∠DPE＝90°，∠PEB＝∠PDC，∠PEB＝∠PBC即可证明PB＝PE，即△PBE为等腰三角形；

（2）①作高线PF，分别计算BE和PF的长，根据三角形面积公式可得y关于x的函数关系式；

②将①中所得二次函数的解析式配方后可得结论．

解：（1）①∵四边形ABCD是正方形，

∴BC＝DC，∠BCD＝90°，AC平分∠BCD．

∴∠BCP＝∠DCP＝45°．

∵PC＝PC，

∴△PBC≌△PDC （SAS）；

②△PBE是等腰三角形，理由是：

由△PBC≌△PDC可知，∠PBC＝∠PDC．

∵∠BCD＝∠DPE＝90°，

∴∠PDC+∠PEC＝180°，

又∠PEB+∠PEC＝180°，

∴∠PEB＝∠PDC，

∴∠PEB＝∠PBC．

∴PB＝PE，即△PBE是等腰三角形．

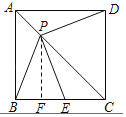
（2）①如图1，过点P作PF⊥BC，垂足为F，则BF＝FE．

∵AP＝x，AC＝，

∴PC＝﹣x，PF＝FC＝

BF＝FE＝1﹣FC＝1﹣（1﹣x）＝x．

∴S△PBE＝＝BFPF＝x（1﹣x）＝．

即

②y＝=

∵a＝﹣＜0，

∴当x＝时，y最大值＝．