题目内容
有两把不同的锁和四把不同的锁,其中两把钥匙恰好分别能打开这两把锁,其余的钥匙不能打开这两把锁,现在任意取出一把钥匙去开任意一把锁,一次就能打开锁的概率是________.

分析:列表得出所有等可能的情况数,找出任意取出一把钥匙去开任意一把锁,一次就能打开锁的情况,即可求出所求的概率.
解答:列表如下:(其中1,2,3,4分别表示四把钥匙,a,b,c,d表示四把锁,1能开启a,2能开启b),
| 1 | 2 | 3 | 4 | |
| a | (1,a) | (2,a) | (3,a) | (4,a) |
| b | (1,b) | (2,b) | (3,b) | (4,b) |
| c | (1,c) | (2,c) | (3,c) | (4,c) |
| d | (1,d) | (2,d) | (3,d) | (4,d) |
所有等可能的情况有16种,任意取出一把钥匙去开任意一把锁,一次就能打开锁的情况有2种,
则P=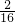 =
= .
.
故答案为:
点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目