题目内容
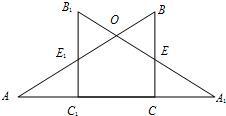 20、如图,两个全等的直角三角形△ABC和△A1B1C1中,∠ACB=∠A1C1B1=90°,两条相等的直角边AC,A1C1在同一直线上,A1B1与AB交于O,AB与B1C1交于E1,A1B1与BC交于E.
20、如图,两个全等的直角三角形△ABC和△A1B1C1中,∠ACB=∠A1C1B1=90°,两条相等的直角边AC,A1C1在同一直线上,A1B1与AB交于O,AB与B1C1交于E1,A1B1与BC交于E.(1)写出图中除△ABC≌△A1B1C1外的所有其它各组全等三角形(不再连线和标注字母);
(2)求证:B1E1=BE.
分析:(1)根据全等三角形的判定:三组对应边分别相等的两个三角形全等(简称SSS);有两边及其夹角对应相等的两个三角形全等(SAS);有两角及其夹边对应相等的两个三角形全等(ASA)可证得;
(2)由1可证得△ACE≌△A1C1E1,可推出CE=C1E1,易证B1E1=BE.
(2)由1可证得△ACE≌△A1C1E1,可推出CE=C1E1,易证B1E1=BE.
解答:解:(1)△ACE≌△A1C1E1,△OBE≌△O1B1E1;
(2)∵△ABC≌△A1B1C1
∴AC=A1C1,BC=B1C1
∴AC1=A1C
已知∠A=∠A1,∠ACE=∠A1C1E1=90°
∴△ACE≌△A1C1E1
∴CE=C1E1
又∵BC=B1C1
∴B1E1=BE.
(2)∵△ABC≌△A1B1C1
∴AC=A1C1,BC=B1C1
∴AC1=A1C
已知∠A=∠A1,∠ACE=∠A1C1E1=90°
∴△ACE≌△A1C1E1
∴CE=C1E1
又∵BC=B1C1
∴B1E1=BE.
点评:三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目
 =6cm.
=6cm.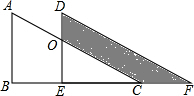 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
 =6cm.
=6cm.