题目内容
如图,已知等腰△AOB放置在平面直角坐标系xOy中, OA=OB,点B的坐标为(3,4) .
(1)求直线AB的解析式;
(2)问将等腰△AOB沿x轴正方向平移多少个单位,能使点B落在反比例函数 (x>0)的图象上.
(x>0)的图象上.

(1)求直线AB的解析式;
(2)问将等腰△AOB沿x轴正方向平移多少个单位,能使点B落在反比例函数
 (x>0)的图象上.
(x>0)的图象上.
(1)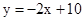 ;(2)5.
;(2)5.
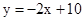 ;(2)5.
;(2)5.试题分析:(1)根据等腰三角形的性质和勾股定理求出点A的坐标,应用待定系数法即可求得直线AB的解析式.
(2)设将等腰△AOB沿x轴正方向平移m个单位,能使点B落在反比例函数
 (x>0)的图象上,根据点在曲线上点的坐标满足方程的关系,将平移后点B的坐标 (
(x>0)的图象上,根据点在曲线上点的坐标满足方程的关系,将平移后点B的坐标 (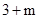 ,4)代入
,4)代入 求出m,即为所求.
求出m,即为所求.(1)如图,过点B作BC⊥x轴于点C.
∵点B的坐标为(3,4),
∴OC=3,BC=4.
∴由勾股定理可得OB="5" .
∵ OA=OB,
∴ 点A的坐标为(5,0).
设直线AB的解析式为
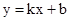 .
.可求直线AB的解析式为
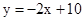 .
.
(2)设将等腰△AOB沿x轴正方向平移m个单位,能使点B落在反比例函数
 (x>0)的图象上,则平移后点B的坐标为(
(x>0)的图象上,则平移后点B的坐标为(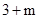 ,4),
,4),将(
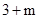 ,4)代入
,4)代入 得
得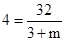 ,解得
,解得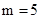 .
.∴将等腰△AOB沿x轴正方向平移5个单位,能使点B落在反比例函数
 (x>0)的图象上.
(x>0)的图象上.
练习册系列答案
相关题目
 与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
 ,若
,若 随
随 的增大而减小,则该函数的图象经过 ( )
的增大而减小,则该函数的图象经过 ( ) 名学生去旅行,甲、乙旅行社的收费分别为
名学生去旅行,甲、乙旅行社的收费分别为 ,
,
 ,到了一个离家900m的阅报亭,看了10
,到了一个离家900m的阅报亭,看了10
 时,函数
时,函数 与
与 在同一坐标系中的图象大致是( )
在同一坐标系中的图象大致是( )