题目内容
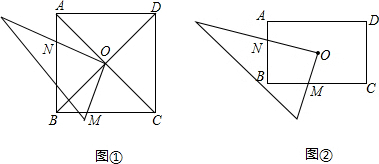
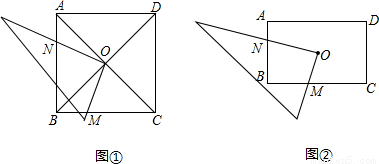
已知:O为四边形ABCD的对角线AC、BD的交点,将直角三角板的直角顶点与O点重合,转动三角板使两直角边始终与BC、AB相交,交点分别为M、N.
(1)若ABCD为正方形,如图①,猜想:线段OM与ON间的大小关系,并证明你的结论;
(2)若ABCD为矩形,如图②,且AB=4,AD=6,OM=x,ON=y,求y与x之间的函数关系式.
(1)OM=ON.
证明:∵四边形ABCD是正方形,
∴OA=OB,∠OAN=∠OBM=45°,∠AOB=90°,
∴∠AON+∠BON=90°,
∵∠BON+∠BOM=90°,
∴∠AON=∠BOM,
在△AON和△BOM中,
∵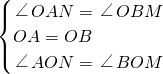 ,
,
∴△AON≌△BOM(ASA),
∴OM=ON;
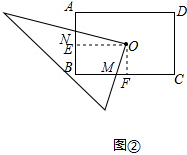
(2)解:过点O作OE⊥AB于点E,作OF⊥BC于点F,
∵四边形ABCD为矩形,AB=4,AD=6,
∴OE= AD=3,OF=
AD=3,OF= AB=2,OE⊥OF,
AB=2,OE⊥OF,
∴∠EOM+∠FOM=90°,
∵∠EON+∠EOM=90°,
∴∠EON=∠FOM,
∵∠OEN=∠OFM=90°,
∴△FOM∽△EON,
∴OM:ON=OF:OE=2:3,
∵OM=x,ON=y,
∴y与x之间的函数关系式为:y= x.
x.
分析:(1)由四边形ABCD为正方形,易证得△AON≌△BOM,然后由全等三角形的性质,证得OM=ON;
(2)首先过点O作OE⊥AB于点E,作OF⊥BC于点F,易证得△FOM∽△EON,然后由相似三角形的对应边成比例,求得y与x之间的函数关系式.
点评:此题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质以及矩形的判定与性质.此题那难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
证明:∵四边形ABCD是正方形,
∴OA=OB,∠OAN=∠OBM=45°,∠AOB=90°,
∴∠AON+∠BON=90°,
∵∠BON+∠BOM=90°,
∴∠AON=∠BOM,
在△AON和△BOM中,
∵
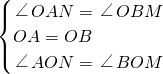 ,
,∴△AON≌△BOM(ASA),
∴OM=ON;

(2)解:过点O作OE⊥AB于点E,作OF⊥BC于点F,
∵四边形ABCD为矩形,AB=4,AD=6,
∴OE=
 AD=3,OF=
AD=3,OF= AB=2,OE⊥OF,
AB=2,OE⊥OF,∴∠EOM+∠FOM=90°,
∵∠EON+∠EOM=90°,
∴∠EON=∠FOM,
∵∠OEN=∠OFM=90°,
∴△FOM∽△EON,
∴OM:ON=OF:OE=2:3,
∵OM=x,ON=y,
∴y与x之间的函数关系式为:y=
 x.
x.分析:(1)由四边形ABCD为正方形,易证得△AON≌△BOM,然后由全等三角形的性质,证得OM=ON;
(2)首先过点O作OE⊥AB于点E,作OF⊥BC于点F,易证得△FOM∽△EON,然后由相似三角形的对应边成比例,求得y与x之间的函数关系式.
点评:此题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质以及矩形的判定与性质.此题那难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE.
如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE.