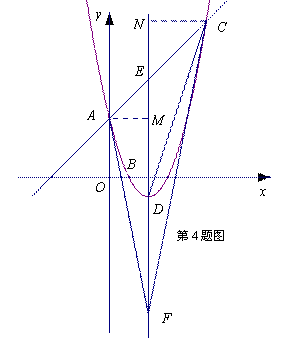
题目内容
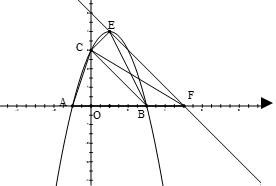
已知抛物线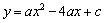 与
与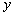 轴交于点
轴交于点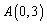 ,点
,点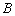 是抛物线上的点,且满足
是抛物线上的点,且满足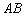 ∥
∥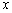 轴,点
轴,点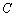 是抛物线的顶点.
是抛物线的顶点.

(1)求抛物线的对称轴及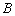 点坐标;
点坐标;
(2)若抛物线经过点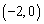 ,求抛物线的表达式;
,求抛物线的表达式;
(3)对(2)中的抛物线,点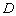 在线段
在线段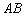 上,若以点
上,若以点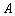 、
、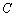 、
、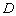 为顶点的三角形与
为顶点的三角形与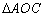 相似,试求点
相似,试求点 的坐标.
的坐标.
【答案】
(1)
(2)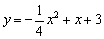
(3)点 的坐标为
的坐标为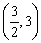 或
或
【解析】解(1)由题意得, ,∴对称轴为直线
,∴对称轴为直线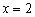 ;…………………(2分)
;…………………(2分)
∵点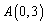 ,点
,点 是抛物线上的点,
是抛物线上的点,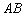 ∥
∥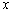 轴,
轴,
∴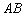 被直线
被直线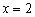 垂直平分,∴
垂直平分,∴ .………………………………………(1分)
.………………………………………(1分)
(2)∵抛物线经过点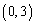 ,
,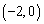 ,所以有
,所以有 ,……………(2分)
,……………(2分)
解得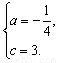 ,∴抛物线的表达式为
,∴抛物线的表达式为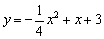 .………………………(1分)
.………………………(1分)
(3)∵抛物线的对称轴为直线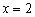 ,∴
,∴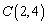 ,…………………………(1分)
,…………………………(1分)
过点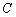 作
作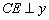 轴,垂足为点
轴,垂足为点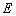 ,设对称轴与
,设对称轴与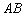 交于点
交于点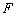 .……………(1分)
.……………(1分)
∵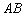 ∥
∥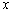 轴,∴
轴,∴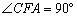 ,∴
,∴ ,
,
又∵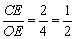 ,
,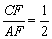 ,∴
,∴ ,∴
,∴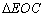 ∽
∽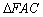 ,…………(1分)
,…………(1分)
∴ ,………………………………………………………………(1分)
,………………………………………………………………(1分)
当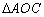 ∽
∽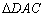 时,有
时,有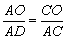 ,
,
∵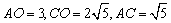 ,∴
,∴ ,∴
,∴ ;…………………(1分)
;…………………(1分)
当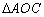 ∽
∽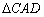 时,有
时,有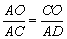 ,
,
∴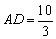 ,∴
,∴ ,………………………………………………………(1分)
,………………………………………………………(1分)
综上所述满足条件的点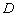 的坐标为
的坐标为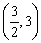 或
或 .
.

练习册系列答案
相关题目

 与
与 轴交于点
轴交于点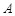 (-1,0)、
(-1,0)、 (3,0),与
(3,0),与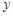 轴的正半轴交于点
轴的正半轴交于点 ,顶点为
,顶点为 .
.
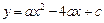 与
与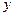 轴交于点
轴交于点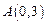 ,点
,点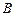 是抛物线上的点,且满足
是抛物线上的点,且满足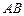 ∥
∥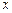 轴,点
轴,点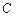 是抛物线的顶点.
是抛物线的顶点.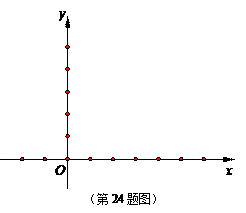
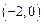 ,求抛物线的表达式;
,求抛物线的表达式;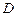 在线段
在线段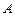 、
、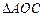 相似,试求点
相似,试求点