Question

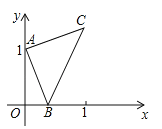
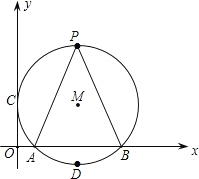
【题目】如图，⊙M与x轴交于A、B两点，与y轴切于点C，且OA，OB的长是方程x2﹣4x+3＝0的解．

（1）求M点的坐标．

（2）若P是⊙M上一个动点（不包括A、B两点），求∠APB的度数．

Answer 1

【答案】(1)（2，）；(2)30°或150°.

【解析】

（1）过点M作ME⊥x轴于点E，连接MA，MC，解出方程后可知OA＝1，OB＝3，然后即可求出OE的长度，由于C是切点，所以MC是半径，又因为MC＝OE，从而可知⊙M的半径，利用垂径定理即可求出M的坐标．

（2）由于点P的位置不确定，需要分两种情况进行讨论，可根据圆周角定理以及圆内接四边形的性质求解．

解：（1）过点M作ME⊥x轴于点E，连接MA，MC，

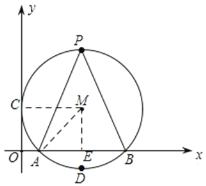
∵OA，OB的长是方程x2﹣4x+3＝0的解，

∴解得x＝1或x＝3，

∴OA＝1，OB＝3，

∴A（1，0），B（3，0）

由垂径定理可知：AE＝BE，

∴E（2，0），

∴OE＝2，AE＝1，

∵⊙M与y轴切于点C，

∴MC⊥OC，

∵ME⊥x轴，y轴⊥x轴，MC、AM是⊙M的半径，

∴MC=AM＝OE＝2，

∴由勾股定理可知：ME=＝，

∴M的坐标为（2，）；

（2）连接MB、AM

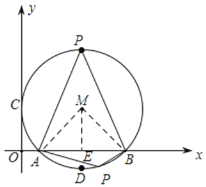
当点P在x轴上方时，

由（1）可知：AM=MB＝2，AB＝3-1=2，

∴∠AMB＝60°，

∴由圆周角定理可知：∠APB＝∠AMB＝30°，

当点P在x轴下方时，

∴由圆内接四边形的性质可知：此时∠APB＝180°﹣30°＝150°．