题目内容
【题目】阅读并探究下列问题:

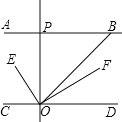
(1)如图1,将长方形纸片剪两刀,其中AB∥CD,则∠2与∠1、∠3有何关系?为什么?
(2)如图2,将长方形纸片剪四刀,其中AB∥CD,则∠2+∠4与∠1+∠3+∠5有何关系?为什么?
(3)如图3,将长方形纸片剪n刀,其中AB∥CD,你又有何发现?
(4)如图4,直线AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=50°,则∠GHM= .
【答案】(1)∠2=∠1+∠3;(2)∠2+∠4=∠1+∠3+∠5;(3)开口向左的角的度数的各等于开口向右的角的度数的和;(4)40°.
【解析】
(1)过E点作EF∥AB,则EF∥CD,根据两直线平行,内错角相等得到∠AEF=∠1,∠CEF=∠3,即有∠2=∠1+∠3;
(2)分别过E、G、F分别作EM∥AB,GN∥AB,FP∥AB,根据两直线平行,内错角相等,同(1)一样易得到∠2+∠4=∠1+∠3+∠5;
(3)综合(1)(2)易得开口向左的角的度数的各等于开口向右的角的度数的和.
(4)利用(3)的结论得到∠BFG+∠GHM+∠MND=∠FGH+∠HMN,易计算出∠GHM.
(1)图1中,∠2=∠1+∠3.理由如下:
过E点作EF∥AB,如图,
则EF∥CD,
∴∠AEF=∠1,∠CEF=∠3,
∴∠2=∠1+∠3
(2)图2中,分别过E、G、F分别作EM∥AB,GN∥AB,FP∥AB,
同(1)的证明方法一样可得∠2+∠4=∠1+∠3+∠5;
(3)图3中,开口向左的角的度数的各等于开口向右的角的度数的和.
(4)图4中,由(3)的结论得,∠BFG+∠GHM+∠MND=∠FGH+∠HMN,
∴30°+∠GHM+50°=90°+30°,
∴∠GHM=40°.
故答案为40°.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目