题目内容
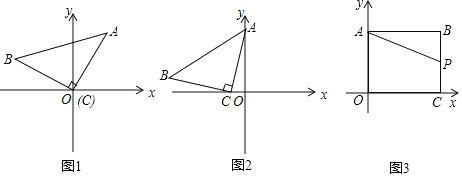
【题目】已知:有理数a、b、c在数轴上的位置如图所示,且|c|>|a|.
![]()
(1)若|a+10|=20,b2=400,c的相反数是30,求a、b、c的值;
(2)在(1)的条件下,a、b、c分别是A、B、C点在数轴上所对应的数,
①线段AC的长是________,将数轴折叠使得点A和点C重合,则折痕处在数轴上表示的数是__________
②数轴上是否存在一点P,使得P点到C点的距离加上P点到A点的距离减去P点到B点的距离为50,即PC+PAPB=50?若存在,求出P点在数轴上所对应的数;若不存在,请说明理由;
③点C,B分别以4个单位/秒和3个单位/秒的速度同时向右运动,点A以7个单位/秒的速度向右运动,是否存在常数m,使得3CA+2mOB-mOA为定值,若存在,请求出m值以及这个定值;若不存在,请说明理由.
【答案】(1)a=10,b=20,c=-30;(2) ①40,-10;②存在;-90或![]() ;(2)存在m=9,定值是390.
;(2)存在m=9,定值是390.
【解析】
(1)利用绝对值的性质和数轴即可求出a,利用b2=400和数轴即可求出b,利用c的相反数即可求出c;
(2)①利用数轴上两点之间的距离公式即可求出AC,再利用中点公式即可求出折痕所表示的数;
②设P表示的数为![]() ,根据P点不同的位置及数轴上两点的距离公式分类讨论即可;
,根据P点不同的位置及数轴上两点的距离公式分类讨论即可;
③设运动时间为t,利用数轴上两点之间的距离公式,表示出CA、OB、OA,将它们代入3CA+2mOB-mOA并化简,再根据其为定值,即与t值无关,令t的系数为0即可.
解:(1)∵|a+10|=20,b2=400,c的相反数是30
解得a=﹣30或10,b=±20,c=﹣30
由数轴可知:a>0,b>0
∴a=10,b=20,c=﹣30
(2)①根据数轴上两点之间的距离公式:AC=| a-c|=40;
若A、C两点重合,则折痕在数轴上所表示的点即为AC的中点,故折痕处在数轴上表示的数是![]() ;
;
②存在,求法如下
假设P点所表示的数为![]() ,
,
当P在C左侧时,即![]() ,如下图所示:
,如下图所示:
![]()
∴PC=﹣30-![]() ,PA=10-
,PA=10-![]() ,PB=20-
,PB=20-![]()
根据PC+PAPB=50,
∴(﹣30-![]() )+(10-
)+(10-![]() )-(20-
)-(20-![]() )=50
)=50
解得:![]() .
.
若P在C、A之间时,即![]() ,如下图所示:
,如下图所示:
![]()
∴PC=![]() ,PA=10-
,PA=10-![]() ,PB=20-
,PB=20-![]()
根据PC+PAPB=50
(![]() )+(10-
)+(10-![]() )-(20-
)-(20-![]() )=50
)=50
解得:![]() ,不符合前提,故舍去;
,不符合前提,故舍去;
若P在A、B之间时,即![]() ,如下图所示:
,如下图所示:
![]()
∴PC=![]() ,PA=
,PA=![]() ,PB=20-
,PB=20-![]()
根据PC+PAPB=50
(![]() )+(
)+(![]() )-(20-
)-(20-![]() )=50
)=50
解得:![]() ;
;
若P在B右侧时,即![]() ,如下图所示:
,如下图所示:
![]()
∴PC=![]() ,PA=
,PA=![]() ,PB=
,PB=![]()
根据PC+PAPB=50
(![]() )+(
)+(![]() )-(
)-(![]() )=50
)=50
解得:![]() ,不符合前提,故舍去;
,不符合前提,故舍去;
综上所述:P点在数轴上所对应的数是:-90或![]() .
.
③存在,理由如下:
设运动时间为t,此时C表示的数为:﹣30+4t,A表示的数为:10+7t,B表示的数为20+3t.
![]()
∴AC=(10+7t)-(﹣30+4t)=3t+40,OA=10+7t,OB=20+3t代入3CA+2mOB-mOA中得:
原式=3(3t+40)+2m(20+3t)-m(10+7t)
=(9-m)t+120+30m
∵3CA+2mOB-mOA为定值,即与t值无关,令t 的系数为0即可,
∴9-m=0,解得:
m=9,代入得:
定值=120+30×9=390.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案【题目】潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积 (单位:亩) | 种植B类蔬菜面积 (单位:亩) | 总收入 (单位:元) |
甲 | 3 | 1 | 12500 |
乙 | 2 | 3 | 16500 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.