题目内容
如图,l1,l2,l3,l4是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为h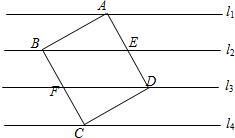 ,正方形ABCD的四个顶点分别在这四条直线上,且正方形ABCD的面积是25.
,正方形ABCD的四个顶点分别在这四条直线上,且正方形ABCD的面积是25.(1)连接EF,证明△ABE、△FBE、△EDF、△CDF的面积相等.
(2)求h的值.
分析:(1)△ABE和△FBE同底同高,因而面积相等,同理△FBE和△EDF的面积相等,△EDF和△CDF的面积相等,因而△ABE、△FBE、△EDF、△CDF的面积相等.
(2)根据正方形的面积就可以求出边长,得到AE,AB的长,根据勾股定理得到BE的长,△ABE的面积是长方形的面积的
,再根据三角形的面积等于
BE•h就可以求出h的长.
(2)根据正方形的面积就可以求出边长,得到AE,AB的长,根据勾股定理得到BE的长,△ABE的面积是长方形的面积的
| 1 |
| 4 |
| 1 |
| 2 |
解答:(1)证明:连接EF,
∵l1∥l2∥l3∥l4,且四边形ABCD是正方形,
∴BE∥FD,BF∥ED,
∴四边形EBFD为平行四边形,
∴BE=FD,(2分)
又∵l1、l2、l3和l4之间的距离为h,
∴S△ABE=
BE•h,S△FBE=
BE•h,
S△EDF=
FD•h,S△CDF=
FD•h,
∴S△ABE=S△FBE=S△EDF=S△CDF.(4分)
(2)解:过A点作AH⊥BE于H点,过E点作EM⊥FD于M点,
方法一:∵S△ABE=S△FBE=S△EDF=S△CDF,
又∵正方形ABCD的面积是25,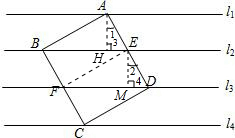
∴S△ABE=
,且AB=AD=5,(7分)
又∵l1∥l2∥l3∥l4,每相邻的两条平行直线间的距离为h,
∴AH=EM=h,
∵AH⊥l2,EM⊥l3,l2∥l3,
∴∠3=∠4=90°,AH∥EM,
∴∠1=∠2,
∴△AHE≌△EMD,
∴AE=DE,
同理:BF=FC,
∴E、F分别是AD与BC的中点,
∴AE=
AD=
,
∴在Rt△ABE中,
BE=
=
,(10分)
又∵AB•AE=BE•AH,
∴AH=
=
=
.(12分)
方法二:不妨设BE=FD=x(x>0),
则S△ABE=S△FBE=S△EDF=S△CDF=
,(6分)
又∵正方形ABCD的面积是25,
∴S△ABE=
xh=
,且AB=5,
则xh=
①,(8分)
又∵在Rt△ABE中:AE=
=
,
又∵∠BAE=90°,AH⊥BE,
∴Rt△ABE∽Rt△HAE,
∴
=
,即
=
,
变形得:(hx)2=25(x2-52)②(10分),
把①两边平方后代入②得:
=25(x2-52)③,
解方程③得x=
(x=-
舍去),
把x=
代入①得:h=
.(12分)
∵l1∥l2∥l3∥l4,且四边形ABCD是正方形,
∴BE∥FD,BF∥ED,
∴四边形EBFD为平行四边形,
∴BE=FD,(2分)
又∵l1、l2、l3和l4之间的距离为h,
∴S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
S△EDF=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABE=S△FBE=S△EDF=S△CDF.(4分)
(2)解:过A点作AH⊥BE于H点,过E点作EM⊥FD于M点,
方法一:∵S△ABE=S△FBE=S△EDF=S△CDF,
又∵正方形ABCD的面积是25,

∴S△ABE=
| 25 |
| 4 |
又∵l1∥l2∥l3∥l4,每相邻的两条平行直线间的距离为h,
∴AH=EM=h,
∵AH⊥l2,EM⊥l3,l2∥l3,
∴∠3=∠4=90°,AH∥EM,
∴∠1=∠2,
∴△AHE≌△EMD,
∴AE=DE,
同理:BF=FC,
∴E、F分别是AD与BC的中点,
∴AE=
| 1 |
| 2 |
| 5 |
| 2 |
∴在Rt△ABE中,
BE=
| AB2+AE2 |
5
| ||
| 2 |
又∵AB•AE=BE•AH,
∴AH=
| AB•AE |
| BE |
5×
| ||||
|
| 5 |
方法二:不妨设BE=FD=x(x>0),
则S△ABE=S△FBE=S△EDF=S△CDF=
| xh |
| 2 |
又∵正方形ABCD的面积是25,
∴S△ABE=
| 1 |
| 2 |
| 25 |
| 4 |
则xh=
| 25 |
| 2 |
又∵在Rt△ABE中:AE=
| BE2-AB2 |
| x2-52 |
又∵∠BAE=90°,AH⊥BE,
∴Rt△ABE∽Rt△HAE,
∴
| AH |
| AB |
| AE |
| BE |
| h |
| 5 |
| ||
| x |
变形得:(hx)2=25(x2-52)②(10分),
把①两边平方后代入②得:
| 252 |
| 4 |
解方程③得x=
5
| ||
| 2 |
5
| ||
| 2 |
把x=
5
| ||
| 2 |
| 5 |
点评:本题主要考查了勾股定理,根据三角形的面积公式得到四个三角形的面积相等是解决本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 22、某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,如图,l1、l2分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,则以下判断错误的是( )
22、某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,如图,l1、l2分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,则以下判断错误的是( )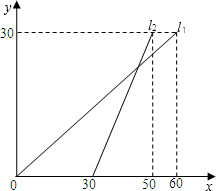 的路程y(千米)随时间x(分钟)变化的函数图象.根据图象,解答下列问题:
的路程y(千米)随时间x(分钟)变化的函数图象.根据图象,解答下列问题:
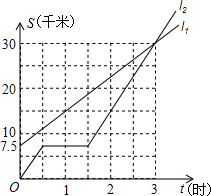 如图,l1、l2分别表示步行者与骑自行车在同一路上行驶的路程S与时间t的关系.
如图,l1、l2分别表示步行者与骑自行车在同一路上行驶的路程S与时间t的关系. 如图,l1,l2分别表示一种白炽灯和一种节能灯的费用y与照明时间x(h)的函数图象,假设两种灯的使用寿命都是2000h,照明效果一样.(费用=灯的售价+电费,单位:元)
如图,l1,l2分别表示一种白炽灯和一种节能灯的费用y与照明时间x(h)的函数图象,假设两种灯的使用寿命都是2000h,照明效果一样.(费用=灯的售价+电费,单位:元)