题目内容
 如图,等边三角形ABC内有一点P,PE⊥AB,PF⊥AC,PD⊥BC,垂足分别为E,F,D,且AH⊥BC于H,试用三角形面积公式证明:PE+PF+PD=AH.
如图,等边三角形ABC内有一点P,PE⊥AB,PF⊥AC,PD⊥BC,垂足分别为E,F,D,且AH⊥BC于H,试用三角形面积公式证明:PE+PF+PD=AH.
分析:本题可通过三角形的面积来求证,连接AP,BP,CP后,分别表示出三角形APB,BPC,APC和三角形ABC的面积,根据三角形ABC的面积等于这三个小三角形的面积和,我们将三个三角形的面积表达式相加后就会得出PE+PF+PD=AH.
解答: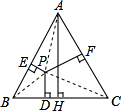 证明:连接AP,BP,CP,
证明:连接AP,BP,CP,
∵PE⊥AB,PF⊥AC,PD⊥BC,AH⊥BC于H,
∴S△ABC=
BC•AH,S△APB=
AB•PE,S△APC=
AC•PF,S△BPC=
BC•PD
∵S△ABC=S△APB+S△APC+S△BPC
∴
BC•AH=
AB•PE+
AC•PF+
BC•PD,且AB=BC=AC,
即PE+PF+PD=AH.
 证明:连接AP,BP,CP,
证明:连接AP,BP,CP,∵PE⊥AB,PF⊥AC,PD⊥BC,AH⊥BC于H,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ABC=S△APB+S△APC+S△BPC
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即PE+PF+PD=AH.
点评:本题考查了等边三角形的性质及三角形的面积等知识;本题直接找线段间的关系不容易得出结论,但是通过分割面积法就容易证得,所以解题时思路要开阔,面积法求线段的关系是很重要的方法,注意掌握.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 已知:如图,等边三角形AOB的顶点A在反比例函数y=
已知:如图,等边三角形AOB的顶点A在反比例函数y= 如图,等边三角形ABC中,D、E分别为AB、BC边上的两动点,且总使AD=BE,AE与CD交于点F,AG⊥CD于点G,则
如图,等边三角形ABC中,D、E分别为AB、BC边上的两动点,且总使AD=BE,AE与CD交于点F,AG⊥CD于点G,则 已知:如图,等边三角形ABC的边长为6,点D,E分别在边AB,AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.
已知:如图,等边三角形ABC的边长为6,点D,E分别在边AB,AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O. 如图,等边三角形ABC的边长为a,若D、E、F、G分别为AB、AC、CD、BF的中点,则△BEG的面积是( )
如图,等边三角形ABC的边长为a,若D、E、F、G分别为AB、AC、CD、BF的中点,则△BEG的面积是( )