题目内容
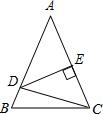 (2012•广东模拟)在△ABC中,已知AB=AC,DE垂直平分AC,∠A=50°,则∠DCB的度数是
(2012•广东模拟)在△ABC中,已知AB=AC,DE垂直平分AC,∠A=50°,则∠DCB的度数是15°
15°
.分析:由DE垂直平分AC,∠A=50°,根据线段垂直平分线的性质,易求得∠ACD的度数,又由AB=AC,可求得∠ACB的度数,继而可求得∠DCB的度数.
解答:解:∵DE垂直平分AC,
∴AD=CD,
∴∠ACD=∠A=50°,
∵AB=AC,∠A=50°,
∴∠ACB=∠B=
=65°,
∴∠DCB=∠ACB-∠ACD=15°.
故答案为:15°.
∴AD=CD,
∴∠ACD=∠A=50°,
∵AB=AC,∠A=50°,
∴∠ACB=∠B=
| 180°-∠A |
| 2 |
∴∠DCB=∠ACB-∠ACD=15°.
故答案为:15°.
点评:此题考查了线段垂直平分线的性质与等腰三角形的性质.此题比较简单,注意数形结合思想的应用.

练习册系列答案
相关题目
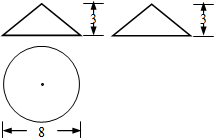 (2012•广东模拟)一个几何体的三视图如图所示,这个几何体侧面展开图的面积是( )
(2012•广东模拟)一个几何体的三视图如图所示,这个几何体侧面展开图的面积是( ) (2012•广东模拟)如图,AB切⊙O于点A,OD⊥弦AC于点D,延长OD,交AB于点B,若∠O=60°,AC=6cm,则AB=
(2012•广东模拟)如图,AB切⊙O于点A,OD⊥弦AC于点D,延长OD,交AB于点B,若∠O=60°,AC=6cm,则AB=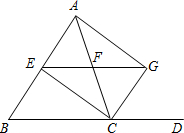 (2012•广东模拟)已知,如图,E、F分别是AB、AC的中点,∠ACD是△ABC的外角,延长EF交∠ACD的平分线于G点,求证:AG⊥CG.
(2012•广东模拟)已知,如图,E、F分别是AB、AC的中点,∠ACD是△ABC的外角,延长EF交∠ACD的平分线于G点,求证:AG⊥CG.