题目内容
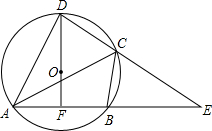 已知:如图,圆内接四边形ABCD的两边AB,DC的延长线相交于点E,DF经过⊙O的圆心,交AB于点F,AB=BE,连接AC,且OD=3,FA=FB=
已知:如图,圆内接四边形ABCD的两边AB,DC的延长线相交于点E,DF经过⊙O的圆心,交AB于点F,AB=BE,连接AC,且OD=3,FA=FB= .
.
(1)求证:△DAC∽△DEA;
(2)求出DA,AC的长度.
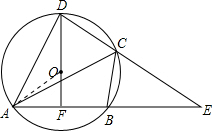 解:(1)∵DF过圆心,且AF=BF,
解:(1)∵DF过圆心,且AF=BF,∴DF⊥AB,
 =
=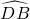 ,
,∴∠ACD=∠EAD,又∠ADC=∠EDA,
∴△DAC∽△DEA;
(2)连接OA,如图所示:
∵DF⊥AB,
∴∠AFD=∠DFE=90°,
在Rt△AOF中,OA=OD=3,AF=
 ,
,根据勾股定理得:OF=
 =2,
=2,∴DF=OD+OF=3+2=5,
在Rt△ADF中,AF=
 ,DF=5,
,DF=5,根据勾股定理得:AD=
 =
= ,
,又EF=FB+BE=FB+AB=3
 ,
,在Rt△DEF中,根据勾股定理得:DE=
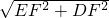 =
=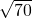 ,
,∴AE=AF+EF=4
 ,
,∵△DAC∽△DEA,
∴
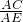 =
= ,即
,即 =
= ,
,则AC=
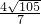 .
.分析:(1)由DF过圆心,且AF=BF,利用垂径定理的逆定理得到DF垂直于AB,且D为优弧ADB的中点,得到两条弧相等,根据等弧所对的圆周角相等可得出一对角相等,再由一对公共角相等,利用两对对应角相等的两三角形相似可得出三角形DAC与三角形DEA相似;
(2)连接OA,由第一问得出DF与AB垂直,得到三角形AOF为直角三角形,根据OA及AF的长,利用勾股定理求出OF的长,再由DF=OD+OF求出DF的长,在直角三角形ADF中,由AF及DF的长,利用勾股定理即可求出AD的长;由AB=BE=2AF=2BF,根据FB的长求出EF的长,在直角三角形DEF中,由DF及EF的长,利用勾股定理求出DE的长,同时根据AF+EF=AE求出AE的长,由第一问的相似三角形,根据相似的性质得出比例式,将各自的值代入即可求出AC的长.
点评:此题考查了垂径定理,勾股定理,圆周角定理,以及相似三角形的判定与性质,垂径定理的内容为:垂直于弦的直径平分于弦,且平分弦所对的弧,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目

 ,
,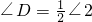 .∵∠1+∠2=360°∴
.∵∠1+∠2=360°∴ ,同理∠BAD+∠BCD=180°,即圆内接四边形对角(相对的两个角)互补.
,同理∠BAD+∠BCD=180°,即圆内接四边形对角(相对的两个角)互补.