题目内容
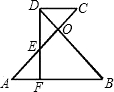 在图中,已知AB∥CD,AO=OB,DF=FB,DF交AC于E.
在图中,已知AB∥CD,AO=OB,DF=FB,DF交AC于E.求证:(1)△DEC∽△OED;(2)ED2=EO•EC.
分析:(1)由于AB∥CD,根据两直线平行内错角相等得出∠A=∠C,∠B=∠CDO,又OA=AB,DF=FB,所以,∠A=∠B,∠B=∠BDF,即:∠BDF=∠C,∠DEO=∠DEO,由相似三角形的判定定理(两角相等,两个三角形相似)即:DEC∽△OED;
(2)根据DEC∽△OED,即可得出
=
,化为等积式即可得证.
(2)根据DEC∽△OED,即可得出
| DE |
| OE |
| EC |
| ED |
解答:证明:(1)∵AB∥CD,
∴∠A=∠C,∠B=∠CDB.
又∵OA=AB,
∴∠A=∠B.
∴∠A=∠C=∠B=∠CDO.
又∵DF=FB,
∴∠B=∠BDF.
∴∠BDF=∠B=∠C.
又∵∠DEO=∠DEO,
∴DEC∽△OED.
(2)∵DEC∽△OED,
∴
=
.
即:ED2=OE•EC.
∴∠A=∠C,∠B=∠CDB.
又∵OA=AB,
∴∠A=∠B.
∴∠A=∠C=∠B=∠CDO.
又∵DF=FB,
∴∠B=∠BDF.
∴∠BDF=∠B=∠C.
又∵∠DEO=∠DEO,
∴DEC∽△OED.
(2)∵DEC∽△OED,
∴
| DE |
| OE |
| EC |
| ED |
即:ED2=OE•EC.
点评:本题主要考查相似三角形的判定定理与性质,关键在于理解清楚题意找出条件判定两个三角形相似,再利用相似三角形的性质即可求解.

练习册系列答案
相关题目
 如图,在△ABC中,已知AB=2a,∠A=30°,CD是AB边的中线,若将△ABC沿CD对折起来,折叠后两个小△ACD与△BCD重叠部分的面积恰好等于折叠前△ABC的面积的
如图,在△ABC中,已知AB=2a,∠A=30°,CD是AB边的中线,若将△ABC沿CD对折起来,折叠后两个小△ACD与△BCD重叠部分的面积恰好等于折叠前△ABC的面积的 如图,在△ABC中,已知AB=8cm,AC=5cm,AD是△ABC的中线,则△ABD的周长比△ACD的周长多
如图,在△ABC中,已知AB=8cm,AC=5cm,AD是△ABC的中线,则△ABD的周长比△ACD的周长多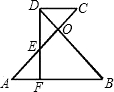 在图中,已知AB∥CD,AO=OB,DF=FB,DF交AC于E.
在图中,已知AB∥CD,AO=OB,DF=FB,DF交AC于E.