题目内容
【题目】(1)若分式![]() 有意义,则x的取值范围是__.
有意义,则x的取值范围是__.
(2)在平面直角坐标系中,点P(﹣4,3)到原点O的距离是____.
(3)有一个三角形的两边长是4和5,要使这个三角形成为直角三角形,则第三边长为_____.
(4)化简![]() 的结果为____.
的结果为____.
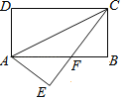
(5)如图,长方形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点E处,且CE与AB交于点F,那么BF=_______.
【答案】x≥﹣5且x≠﹣3 5 ![]() 或3 2+
或3 2+![]() 3
3
【解析】
(1)根据分式与二次根式的有意义的条件即可求解;
(2)根据勾股定理即可求解;
(3)根据勾股定理分情况讨论即可求解;
(4)根据幂的运算法则及平方差公式即可求解;
(5)利用翻折变换的性质及矩形的性质证明AF=CF,得到△ACF是等腰三角形,再勾股定理列出关于线段BF的方程即可解决问题.
(1)依题意得![]() ≥0且
≥0且![]() ≠0
≠0
解得x≥﹣5且x≠﹣3
故答案为:x≥﹣5且x≠﹣3;
(2)点P(﹣4,3)到原点O的距离是![]()
故答案为:5;
(3)①当第三边为斜边时,第三边=![]() ;
;
②当边长为5的边为斜边时,第三边=![]() =3
=3
故答案为:![]() 或3;
或3;
(4)![]()
=![]()
=![]()
=2+![]()
故答案为:2+![]() ;
;
(5)由题意得:△ACD≌△ACE,
∴∠DCA=∠FCA;
又∵四边形ABCD为长方形,
∴CD∥AB,
∴∠DCA=∠CAB,
∴∠FCA=∠CAB,
∴AF=CF,
∴△ACF是等腰三角形,
设BF=x,
则AF=8x=CF,
在Rt△BCF中,由勾股定理得:(8x)2=x2+42,
解得:x=3,
即BF的长为3,
故答案为:3.

练习册系列答案
相关题目