题目内容
 (2013•新余模拟)如图,△ABC是一个直角三角形,其中∠C=90゜,∠A=30°,BC=6;O为AB上一点,且OB=3,⊙O是一个以O为圆心、OB为半径的圆;现有另一半径为3
(2013•新余模拟)如图,△ABC是一个直角三角形,其中∠C=90゜,∠A=30°,BC=6;O为AB上一点,且OB=3,⊙O是一个以O为圆心、OB为半径的圆;现有另一半径为3| 3 |
3
+3或12+3
或12+6
| 3 |
| 3 |
| 3 |
3
+3或12+3
或12+6
.| 3 |
| 3 |
| 3 |
分析:分别从①在B→A的过程中,②在A→C的过程中,③当C与D重合时去分析求解,利用含30°角的直角三角形的性质与圆与圆的外切的性质,即可求得答案.
解答: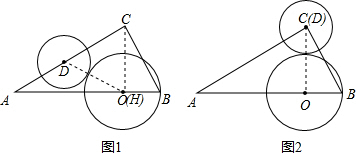 解:①在B→A的过程中,当OD=3+3
解:①在B→A的过程中,当OD=3+3
-3=3
时,⊙D与⊙O外切,此时BD=OB+OD=3+3
,
即t=3+3
;
②如图1,在A→C的过程中,过点C作CH⊥AB于H,连接OD,OC,
∵∠C=90゜,∠A=30°,BC=6,
∴AB=2BC=12,AC=
=6
,
∴∠B=60°,
∴BH=BC•cos∠B=6×
=3,CH=BC•sin∠B=3
,
∵OB=3,
∴O与H重合,
即OC⊥AB,OC=3
,
∴∠BOC=90°-∠B=60°,
∵OD=3
,
∴OC=OD,
∴△OCD是等边三角形,
∴CD=OD=3
,
∴AB+AD=AB+AC-CD=12+6
-3
=12+3
,
即t=12+3
;
③∵由②得,OC=3
=OD,
∴当C与D重合时,⊙D与⊙O外切;
即t=12+6
;
综上,当⊙D与⊙O外切时,t的值为3+3
或12+3
或12+6
.
故答案为:3+3
或12+3
或12+6
.
 解:①在B→A的过程中,当OD=3+3
解:①在B→A的过程中,当OD=3+3| 3 |
| 3 |
| 3 |
即t=3+3
| 3 |
②如图1,在A→C的过程中,过点C作CH⊥AB于H,连接OD,OC,
∵∠C=90゜,∠A=30°,BC=6,
∴AB=2BC=12,AC=
| BC |
| tan30° |
| 3 |
∴∠B=60°,
∴BH=BC•cos∠B=6×
| 1 |
| 2 |
| 3 |
∵OB=3,
∴O与H重合,
即OC⊥AB,OC=3
| 3 |
∴∠BOC=90°-∠B=60°,
∵OD=3
| 3 |
∴OC=OD,
∴△OCD是等边三角形,
∴CD=OD=3
| 3 |
∴AB+AD=AB+AC-CD=12+6
| 3 |
| 3 |
| 3 |
即t=12+3
| 3 |
③∵由②得,OC=3
| 3 |
∴当C与D重合时,⊙D与⊙O外切;
即t=12+6
| 3 |
综上,当⊙D与⊙O外切时,t的值为3+3
| 3 |
| 3 |
| 3 |
故答案为:3+3
| 3 |
| 3 |
| 3 |
点评:此题考查了圆与圆的位置关系,直角三角形的性质以及三角函数的性质.此题难度适中,注意掌握数形结合思想与分类讨论思想的应用.

练习册系列答案
相关题目
 (2013•新余模拟)如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是
(2013•新余模拟)如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是 (2013•新余模拟)如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是
(2013•新余模拟)如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是 (2013•新余模拟)如图,已知AB∥CD,∠A=50°,∠C=∠E.则∠C=
(2013•新余模拟)如图,已知AB∥CD,∠A=50°,∠C=∠E.则∠C=