题目内容
 24、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O.
24、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O.(1)设AD与BC交于点P,BE与CD交于点Q,连接PQ、以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.恒成立的结论有
①②③⑤
(把你认为正确的序号都填上)(2)在你认为恒成立的结论中选一个加以证明.
分析:根据等边三角形的性质及全等三角形的判定定理进行逐一判断即可.
①根据等边三角形三边相等及三角形内角和外角的关系求出△ACD≌△BCE,再根据全等三角形的性质解答即可;
②根据,△ABC为等边三角形及△ACP≌△BCQ可求出△PCQ为等边三角形,再根据平行线的判定定理即可解答;
③根据PQ∥AE可求出△APC≌△BPQ,再根据全等三角形的性质即可解答;
④根据在同一三角形中等边对等角解答;
⑤根据等边三角形的性质及三角形内角和定理解答.
①根据等边三角形三边相等及三角形内角和外角的关系求出△ACD≌△BCE,再根据全等三角形的性质解答即可;
②根据,△ABC为等边三角形及△ACP≌△BCQ可求出△PCQ为等边三角形,再根据平行线的判定定理即可解答;
③根据PQ∥AE可求出△APC≌△BPQ,再根据全等三角形的性质即可解答;
④根据在同一三角形中等边对等角解答;
⑤根据等边三角形的性质及三角形内角和定理解答.
解答:解:①正确,∵△ABC与△DCE为等边三角形,
∴CD=CE,AC=BC,∠ACD=∠BCE=120°,
∴△ACD≌△BCE,
∴AD=BE.
②正确,
∵△ABC为等边三角形,
∴AC=BC,∠ACB=∠DCE=60°,
又∵∠BCD=180°-∠ACB-∠DCE=180°-60°-60°=60°,
又∵△ACD≌△BCE,
∴∠DAE=∠CBE,
∴△ACP≌△BCQ,
∴PC=CQ,
∴△PCQ为等边三角形,
∴∠PQC=∠QCE=60°
∴PQ∥AE.
③正确,
∵△PQC是等边三角形,
∴CQ=CP,
又∵∠ACP=∠BCQ,AC=BC,
∴△APC≌△BQC,
∴AP=BQ.
④错误,∵DC=DE,∠PCQ=∠CPQ=60°,
∴∠DPC>60°,
∴DP≠DC,即DP≠DE.
⑤正确,
∵∠CAP=∠OBP,∠BAC=60°,
∴∠BAP+∠OBP=60°,
又∵∠BAC=60°,
∴∠AOB=180°-(∠BAP+OBP)-∠BAC=60°.
故填①②③⑤.
∴CD=CE,AC=BC,∠ACD=∠BCE=120°,
∴△ACD≌△BCE,
∴AD=BE.
②正确,
∵△ABC为等边三角形,
∴AC=BC,∠ACB=∠DCE=60°,
又∵∠BCD=180°-∠ACB-∠DCE=180°-60°-60°=60°,
又∵△ACD≌△BCE,
∴∠DAE=∠CBE,
∴△ACP≌△BCQ,
∴PC=CQ,
∴△PCQ为等边三角形,
∴∠PQC=∠QCE=60°
∴PQ∥AE.
③正确,
∵△PQC是等边三角形,
∴CQ=CP,
又∵∠ACP=∠BCQ,AC=BC,
∴△APC≌△BQC,
∴AP=BQ.
④错误,∵DC=DE,∠PCQ=∠CPQ=60°,
∴∠DPC>60°,
∴DP≠DC,即DP≠DE.
⑤正确,
∵∠CAP=∠OBP,∠BAC=60°,
∴∠BAP+∠OBP=60°,
又∵∠BAC=60°,
∴∠AOB=180°-(∠BAP+OBP)-∠BAC=60°.
故填①②③⑤.
点评:此题考查了等边三角形的性质、平行线的判定定理、全等三角形的判定与性质及三角形的内角和定理;找着选项的正误是正确解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 24、如图,C为线段AE上一动点,(不与A,E重合),在AE同侧分别作等边三角形ABC和CDE.则以下结论:①AD=BE ②CP=CQ ③AP=BQ ④DE=DP ⑤PQ∥AE中正确的有
24、如图,C为线段AE上一动点,(不与A,E重合),在AE同侧分别作等边三角形ABC和CDE.则以下结论:①AD=BE ②CP=CQ ③AP=BQ ④DE=DP ⑤PQ∥AE中正确的有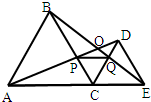 10、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( )
10、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( ) 15、如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是( )
15、如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是( ) 如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.
如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ. 如图,C为线段AE上一动点(不与A,E重合)在AE同侧分别作等边△ABC和等边△CDE,AD与BE相交于点O,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.请你写出三个正确的结论:
如图,C为线段AE上一动点(不与A,E重合)在AE同侧分别作等边△ABC和等边△CDE,AD与BE相交于点O,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.请你写出三个正确的结论: