题目内容
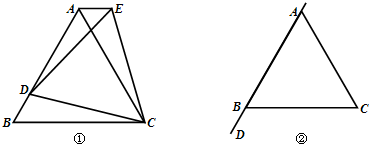
21、(1)如图①,△ABC是等边三角形,D是AB上一点,以CD为一边向上作等边△ECD,连接AE,求证:∠CAE=∠CBA.
(2)在上题(1)中,当D点在AB的延长线上时,其他条件不变,如图②所示,请你补画出题意的图形,(1)的结论还成立吗?若成立,请给予证明;若不成立,请简要说明理由.
(2)在上题(1)中,当D点在AB的延长线上时,其他条件不变,如图②所示,请你补画出题意的图形,(1)的结论还成立吗?若成立,请给予证明;若不成立,请简要说明理由.

分析:(1)根据△ABC与△EDC是等边三角形,利用其三边相等和三角相等的关系,先证∠BCD=∠ACE,然后即可证明结论
(2)同(1)根据△ABC与△EDC是等边三角形,利用其三边相等和三角相等的关系,证明△ACE≌△BCD说明.
(2)同(1)根据△ABC与△EDC是等边三角形,利用其三边相等和三角相等的关系,证明△ACE≌△BCD说明.
解答:解:(1)证明:∵△ABC与△EDC是等边三角形,
∴∠ACB=∠DCE=60°,AC=BC,DC=EC.
又∵∠BCD=∠ACB-∠ACD,∠ACE=∠DCE-∠ACD,
∴∠BCD=∠ACE,
∴△ACE≌△BCD,
∴∠CAE=∠CBA.
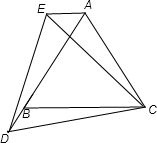
(2)不成立;
因为同(1)易证△ACE≌△BCD,
所以∠CAE=∠CBD,
∠CBD与∠CBA互补,
所以∠CAE和∠CBA互补但不相等.
∴∠ACB=∠DCE=60°,AC=BC,DC=EC.
又∵∠BCD=∠ACB-∠ACD,∠ACE=∠DCE-∠ACD,
∴∠BCD=∠ACE,
∴△ACE≌△BCD,
∴∠CAE=∠CBA.
(2)不成立;
因为同(1)易证△ACE≌△BCD,
所以∠CAE=∠CBD,
∠CBD与∠CBA互补,
所以∠CAE和∠CBA互补但不相等.

点评:此题考查的知识点是等百年三角形的性质,等边三角形各边长相等、各内角为60°的性质,本题中求证△AE≌△BCD是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 如图,如果AB∥CD,那么下面说法错误的是( )
如图,如果AB∥CD,那么下面说法错误的是( ) 如图,直线AB、CD、MN相交于O,∠DOB=60°,BO⊥FO,OM平分∠DOF.
如图,直线AB、CD、MN相交于O,∠DOB=60°,BO⊥FO,OM平分∠DOF. 如图,直线AB、CD被直线CE所截.
如图,直线AB、CD被直线CE所截.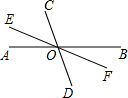 如图,直线AB、CD、EF相交于点O,∠COE=2∠AOE,已知∠BOC=105°,那么∠BOF=( )
如图,直线AB、CD、EF相交于点O,∠COE=2∠AOE,已知∠BOC=105°,那么∠BOF=( ) 如图,直线AB.CD相交于点O,OM⊥AB,NO⊥CD.
如图,直线AB.CD相交于点O,OM⊥AB,NO⊥CD.