题目内容
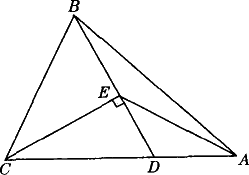
如图,△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连结AE.
(1)写出图中所有相等的线段,并加以证明;
(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;
(3)求△BEC与△BEA的面积之比.
答案:
解析:
解析:
|
(1)EC=EA=EB,DE=DA ∵∠DEC=90°,∠BDC=60°,∠DCE=30°∴DE= ∴∠DEA=∠DAE,又∠EDC=∠DEA+∠DAE=60° ∴∠DEA=∠DAE=30° 又∠BAC=45°∴∠EAB=∠BAC-∠DAE=15° 而∠DEA=∠EAB+∠EBA∴∠EBA=15° ∴∠EBA=∠EAB∴EA=EB ∵∠DCE=∠DAE=30° ∴EC=EA∴EC=EA=EB (2)△ADE∽△CEA或△BCD∽△ACB (3)过点A作AF⊥BD,交BD的延长线于点F, 则∠AFD=∠CED=90°,又∠ADF=∠CDE∴△CED∽△AFD ∴ ∴ |

练习册系列答案
相关题目
 =2
=2 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB. 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( ) 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.