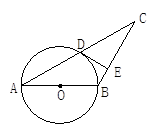题目内容
已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.

答案:
解析:
提示:
解析:
|
∵BD⊥AE 于D,CE⊥AE于E,∴∠ADB =∠AEC=90°,∵∠BAC =90°,∴∠ABD +∠BAD=∠CAE+∠BAD,∴∠ABD =∠CAE; 在△ABD和△CAE中,
∴△ABD≌△CAE(AAS) .∴BD =AE,AD=CE.∵AE =AD+DE,∴BD =CE+DE. |
提示:
|
要证 BD=DE+CE,考虑证明△ABD和△CAE全等. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
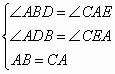
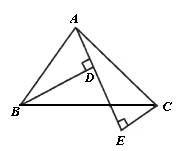
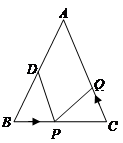
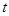 秒.
秒.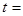 1秒时,则BP= 厘米;
1秒时,则BP= 厘米;