题目内容
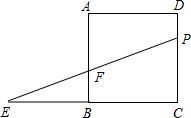 如图,正方形ABCD的边长为10cm,点E在边CB的延长线上,且EB=10cm,点P在边DC上运动,EP与AB的交点为F.设DP=xcm,△EFB与四边形AFPD的面积和为ycm2,那么,y与x之间的函数关系式是
如图,正方形ABCD的边长为10cm,点E在边CB的延长线上,且EB=10cm,点P在边DC上运动,EP与AB的交点为F.设DP=xcm,△EFB与四边形AFPD的面积和为ycm2,那么,y与x之间的函数关系式是分析:易得BF是△EPC的中位线,那么△EFB的面积与△EPC面积之比为1:4,易得正方形的面积,那么也就可以求得四边形AFPD的面积,让△EFB与四边形AFPD的面积相加即可.
解答:解:∵正方形ABCD的边长为10cm,DP=xcm,
∴PC=10-x,
∵EB=10cm,
∴S△EPC=
×(10-x)×(10+10)=100-10x,
BF是△EPC的中位线,
∴△EFB∽△EPC,
∴S△EFB=
×(100-10x),
∴四边形BCPF的面积
×(100-10x),
∵正方形的面积为100,
四边形AFPD的面积=100-
×(100-10x),
∴y=
×(100-10x)+100-
×(100-10x)=5x+50,
故答案为y=5x+50.
∴PC=10-x,
∵EB=10cm,
∴S△EPC=
| 1 |
| 2 |
BF是△EPC的中位线,
∴△EFB∽△EPC,
∴S△EFB=
| 1 |
| 4 |
∴四边形BCPF的面积
| 3 |
| 4 |
∵正方形的面积为100,
四边形AFPD的面积=100-
| 3 |
| 4 |
∴y=
| 1 |
| 4 |
| 3 |
| 4 |
故答案为y=5x+50.
点评:考查了列一次函数问题,用到的知识点为:相似三角形的面积比等于相似比的平方.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 19、如图:正方形ABCD,M是线段BC上一点,且不与B、C重合,AE⊥DM于E,CF⊥DM于F.求证:AE2+CF2=AD2.
19、如图:正方形ABCD,M是线段BC上一点,且不与B、C重合,AE⊥DM于E,CF⊥DM于F.求证:AE2+CF2=AD2. 如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE=
如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE= 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( ) 17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是
17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是 如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.
如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.