题目内容
 一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=-
一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=-| 1 |
| 2 |
| 1 |
| 2 |
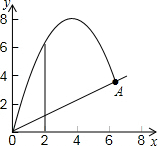
(1)在直角坐标系中画出球的抛出路线草图.当小球离点O的水平距离为多少时,小球离斜坡的铅垂高度(即小球离点O的水平距离为x时的高度减去此时斜坡的高度)是2;
(2)当小球离点O的水平距离为多少时,小球离斜坡的铅垂高度达到最大,并求出这个最大值.
分析:(1)根据抛物线解析式,画出抛物线的图象,并根据铅垂高度的定义,得出方程,解出即可得出答案;
(2)利用配方法求出二次函数的最大值即可.
(2)利用配方法求出二次函数的最大值即可.
解答:解:(1)利用描点法在直角坐标系中画出球的抛出路线草图如下:
设小球离斜坡的铅垂高度为z,则z=-
(x-4)2+8-
x,
即z=-
x2+
x,
依题意得:-
x2+
x=2,
解得:x1=
,x2=
,
所以当小球离点O的水平距离为
或
时,小球离斜坡的铅垂高度是2.
(2)∵z=-
x2+
x,
∴z=-
(x-
)2+
,
故当小球离点O的水平距离为
时,小球离斜坡的铅垂高度最大,最大值是
.

设小球离斜坡的铅垂高度为z,则z=-
| 1 |
| 2 |
| 1 |
| 2 |
即z=-
| 1 |
| 2 |
| 7 |
| 2 |
依题意得:-
| 1 |
| 2 |
| 7 |
| 2 |
解得:x1=
7+
| ||
| 2 |
7-
| ||
| 2 |
所以当小球离点O的水平距离为
7+
| ||
| 2 |
7-
| ||
| 2 |
(2)∵z=-
| 1 |
| 2 |
| 7 |
| 2 |
∴z=-
| 1 |
| 2 |
| 7 |
| 2 |
| 49 |
| 8 |
故当小球离点O的水平距离为
| 7 |
| 2 |
| 49 |
| 8 |
点评:本题考查了二次函数的应用,解答本题的关键是仔细审题,理解铅垂高度的定义,注意掌握配方法求二次函数最值得应用,难度一般.

练习册系列答案
相关题目
 次函数y=
次函数y= 如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数
如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数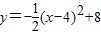 刻画,斜坡(OA)可以用一次函数
刻画,斜坡(OA)可以用一次函数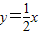 刻画.
刻画.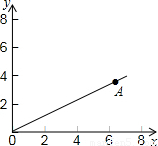
 x2的图象表示,斜坡可以用一次函数y=
x2的图象表示,斜坡可以用一次函数y= x的图象表示.
x的图象表示.