题目内容
如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.如:平行四边形的一条对线所在的直线就是平行四边形的一条面积等分线.
(1)三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的有___;
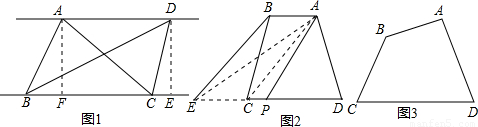
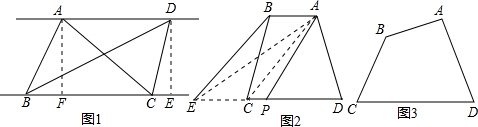
(2)如图1,梯形ABCD中,AB∥DC,如果延长DC到E,使CE=AB,连接AE,那么有S梯形ABCD=S△ADE.请你给出这个结论成立的理由,并过点A作出梯形ABCD的面积等分线(不写作法,保留作图痕迹);
(3)如图,四边形ABCD中,AB与CD不平行,S△ADC>S△ABC,过点A能否作出四边形ABCD的面积等分线?若能,请画出面积等分线,并给出证明;若不能,说明理由.

(1)略
(2)略
(3)能
解析:(1)中线所在的直线.
(2)法一:连接BE,∵AB∥CE,AB=CE,∴四边形ABEC为平行四边形.∴BE∥AC,
∴△ABC和△AEC的公共边AC上的高也相等,∴S△ABC=S△AEC .
∴S梯形ABCD=S△ACD+S△ABC=S△ACD+S△AEC=S△AED .
法二:设AE与BC相交于点F.∵AB∥CE,∴∠ABF=∠ECF,∠BAF=∠CEF.
又∵AB=CE,∴△ABF≌△ECF.∴S梯形ABCD=S四边形AFCD+S△ABF=S四边形AFCD+S△ECF=S△AED .
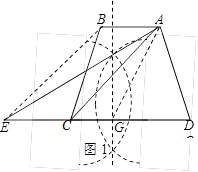
过点A的梯形ABCD的面积等分线的画法如图①所示.
(3)能.连接AC,过点B作BE∥AC交DC的延长线于点E,连接AE.
∵BE∥AC,∴△ABC和△AEC的公共边AC上的高也相等,∴S△ABC=S△AEC .
∴S梯形ABCD=S△ACD+S△ABC=S△ACD+S△AEC=S△AED .
∵S△ACD>S△ABC ,∴面积等分线必与CD相交,取DE中点F,则直线AF即为要求作的四边形ABCD的面积等分线.作图如图②所示.

 ×BC×AF,S△BCD=
×BC×AF,S△BCD=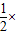 BC×DE
BC×DE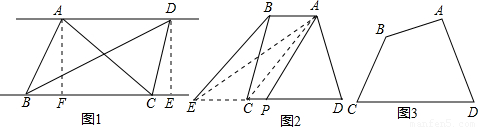
 ×BC×AF,S△BCD=
×BC×AF,S△BCD=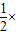 BC×DE
BC×DE