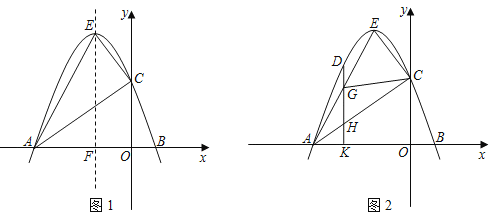Question

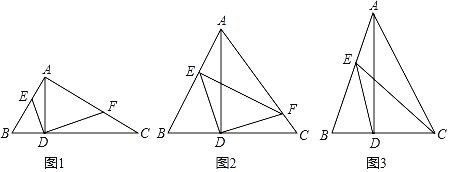
【题目】△ABC中，AD⊥BC，E，F分别在AB，AC上．

（1）已知：DE⊥DF

①如图1：若AB⊥AC，求证：△DAE～△DFC．

②连EF，若FE⊥AB于E（如图2），且BD：CD：DA＝2：3：4，EF＝4，求BC的长．

（2）连EC，DE平分∠BEC（如图3），且AD＝2CD，CE＝2AE，若DE＝10，求AC的长．

Answer 1

【答案】（1）①详见解析；②；（2）2．

【解析】

（1）①由互余的性质可求∠ADE＝∠CDF，∠DAE＝∠C，即可证△DAE～△DFC；

②由BD：CD：DA＝2：3：4，可设BD＝2k，CD＝3k，DA＝4k，作CG⊥AB，得：FE∥CG，由对应线段成比例可得：AE：AF＝1：，求出AE，AF，再由△CFN∽△CAD，△DME∽△DNF即可求解；

（2）由于CE＝2AE，可取EC中点K，连接AK交BC于H，过点E作EM⊥AH于M，过点D作DN⊥AH于N，应用等腰三角形性质和角平分线易证AH∥DE，△CKH∽△CED，△DHN∽△AHD，再结合勾股定理可求得AC．

证明：（1）①如图1，

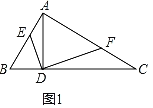
∵DE⊥DF，AD⊥BC，AB⊥AC，

∴∠BAD+∠DAC＝90°，∠DAC+∠C＝90°，∠ADF+∠ADE＝90°，∠ADF+∠CDF＝90°

∴∠ADE＝∠CDF，∠DAE＝∠C

∴△DAE～△DFC

②如图2，过点C作CG⊥AB于G，过点E作EM⊥AD于M，过点F作FN⊥BC于N，

∵BD：CD：DA＝2：3：4，可设BD＝2k，CD＝3k，DA＝4k，

由勾股定理得：AB2k，AC5k

∵BC＝AC＝5k，CG⊥AB

∴AG＝BGABk

∵FE⊥AB

∴FE∥CG

∴

设AEm，AF＝5m，由勾股定理得：AE2+EF2＝AF2，即：（5m）2，

解得：m1＝﹣2（舍去），m2＝2；

∴AE＝2，AF＝10，

∵EM⊥AD，AD⊥BC，

∴△AEM∽△ABD，

，即：

∴EM＝2，AM＝4

∵AD⊥BC，FN⊥BC

∴△CFN∽△CAD

∴，即：

∴FN＝4k﹣8，CN＝3k﹣6

∴DN＝CD﹣CN＝6

∵DE⊥DF，AD⊥BC

∴∠EDM+∠FDM＝∠FDN+∠FDM＝90°

∴∠EDM＝∠FDN

∵∠DME＝∠DNF＝90°

∴△DME∽△DNF

∴，即：，解得：，（舍去）；

∴BD＝25，CD＝3，BC＝5

（2）取EC中点K，连接AK交BC于H，过点E作EM⊥AH于M，过点D作DN⊥AH于N，如图3：

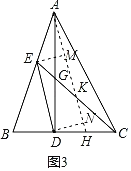
∵CE＝2AE＝2EK

∴AE＝EK

∴∠BAH＝∠AKE

∵∠BEC＝∠BAH+∠AKE

∴∠BEC＝2∠BAH

∵DE平分∠BEC

∴∠BEC＝2∠BED

∴∠BED＝∠BAH

∴AH∥ED

∴△CKH∽△CED，∠GAK＝∠GDE

∴，即：

∴KH＝5，CHCD

∵EM⊥AH，DN⊥AH

∴EM∥DN，∠EMN＝∠DNM＝90°

∵AH∥ED

∴∠EDN＝90°

∴DEMN是矩形，

∴MN＝DE＝10

∵AK＝EK，EM⊥AK

∴AM＝MK

∵AD＝2CD，设CD＝2m，则DH＝m，AD＝4m，AHm，DNm，

∵AD⊥BC，DH⊥AH

∴△DHN∽△AHD

∴，即：HNm，KN＝5m，AM＝MK＝5m，AH＝AM+MN+HN＝5m+10m＝15m

∵AD2+DH2＝AH2

∴（4m）2+m2，解得：（舍去），

∴CD＝2，AD＝4，

∴AC2．