题目内容
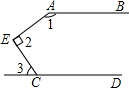如图AB∥CD，∠1=140°，∠2=90°，则∠3的度数是
- A.40°
- B.45°
- C.50°
- D.60°
C
分析：作平行线，把∠2分解成两个角，再两次应用平行线的性质求出∠3．
解答：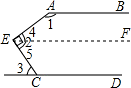
解：过E作直线EF∥AB，
∵AB∥BC，
∴EF∥CD；
∴∠1+∠4=180°，
又∠1=140°，
∴∠4=40°，
∵∠2=90°，
∴∠5=90°-∠4=90°-40°=50°．
∵EF∥CD，
∴∠3=∠5=50°．
故选C．
点评：通过作辅助线，把所求的角转化为已知角的一部分，然后利用平行线性质求解．
分析：作平行线，把∠2分解成两个角，再两次应用平行线的性质求出∠3．
解答：
解：过E作直线EF∥AB，∵AB∥BC，
∴EF∥CD；
∴∠1+∠4=180°，
又∠1=140°，
∴∠4=40°，
∵∠2=90°，
∴∠5=90°-∠4=90°-40°=50°．
∵EF∥CD，
∴∠3=∠5=50°．
故选C．
点评：通过作辅助线，把所求的角转化为已知角的一部分，然后利用平行线性质求解．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
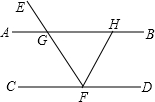已知：如图AB∥CD，EF交AB于G，交CD于F，FH平分∠EFD，交AB于H，∠AGE=50°，求：∠BHF的度数．
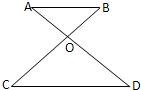4、如图AB∥CD，AD、BC交于点O，∠A=42°，∠C=58°，则∠AOB=（ ）
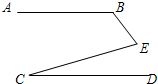4、如图AB∥CD，∠ABE=120°，∠ECD=25°，则∠E=（ ）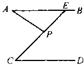
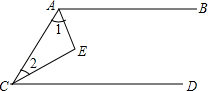完成填空，如图AB∥CD，AE平分∠BAC，CE平分∠ACD．求证：AE⊥CE．