题目内容
甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题:
(1)线段CD表示轿车在途中停留了 h;
(2)求线段DE对应的函数解析式;
(3)求轿车从甲地出发后经过多长时间追上货车.
(1)线段CD表示轿车在途中停留了 h;
(2)求线段DE对应的函数解析式;
(3)求轿车从甲地出发后经过多长时间追上货车.

解:(1)0.5。
(2)设线段DE对应的函数解析式为y=kx+b(2.5≤x≤4.5),
∵D点坐标为(2.5,80),E点坐标为(4.5,300),
∴代入y=kx+b,得: ,解得:
,解得: 。
。
∴线段DE对应的函数解析式为:y=110x-195(2.5≤x≤4.5)。
(3)设线段OA对应的函数解析式为y=mx(0≤x≤5),
∵A点坐标为(5,300),代入解析式y=mx得,300=5m,解得:m=60。
∴线段OA对应的函数解析式为y=60x(0≤x≤5)
由60x=110x-195,解得:x=3.9。
答:轿车从甲地出发后经过3.9小时追上货车。
(2)设线段DE对应的函数解析式为y=kx+b(2.5≤x≤4.5),
∵D点坐标为(2.5,80),E点坐标为(4.5,300),
∴代入y=kx+b,得:
 ,解得:
,解得: 。
。∴线段DE对应的函数解析式为:y=110x-195(2.5≤x≤4.5)。
(3)设线段OA对应的函数解析式为y=mx(0≤x≤5),
∵A点坐标为(5,300),代入解析式y=mx得,300=5m,解得:m=60。
∴线段OA对应的函数解析式为y=60x(0≤x≤5)
由60x=110x-195,解得:x=3.9。
答:轿车从甲地出发后经过3.9小时追上货车。
一次函数的应用,待定系数法,直线上点的坐标与方程的关系。
【分析】(1)利用图象得出CD这段时间为2.5-2=0.5,得出答案即可。
(2)由D点坐标(2.5,80),E点坐标(4.5,300),用待定系数法求出线段DE对应的函数
解析式。
(3)用待定系数法求出OA的解析式,列60x=110x-195时,求解即为轿车追上货车的时间。
【分析】(1)利用图象得出CD这段时间为2.5-2=0.5,得出答案即可。
(2)由D点坐标(2.5,80),E点坐标(4.5,300),用待定系数法求出线段DE对应的函数
解析式。
(3)用待定系数法求出OA的解析式,列60x=110x-195时,求解即为轿车追上货车的时间。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的图象分别与
的图象分别与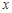 轴、
轴、 轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.求过B、C两点直线的解析式.
轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.求过B、C两点直线的解析式.
 (元) 、
(元) 、 (元)与印制数量
(元)与印制数量 (本)之间的关系式;
(本)之间的关系式;  轴上,顶点B的坐标为(4,6).若直线
轴上,顶点B的坐标为(4,6).若直线 将□ABCO分割成面积相等的两部分,则k的值是( )
将□ABCO分割成面积相等的两部分,则k的值是( )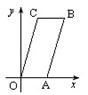


 (cm)与燃烧时间
(cm)与燃烧时间 (h)的关系如图所示. 请根据图像所提供的信息解答下列各问题:
(h)的关系如图所示. 请根据图像所提供的信息解答下列各问题:
 和
和 的图象交于点P,则二元一次方程组
的图象交于点P,则二元一次方程组 的解是 .
的解是 .

 ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低? 是正比例函数,则常数m的值是 .
是正比例函数,则常数m的值是 .