题目内容
如图1所示,点C将线段AB分成两部分,如果| AC |
| AB |
| BC |
| AC |
| s1 |
| s |
| s2 |
| s1 |
(1)研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点,如图2所示,则
 直线CD是△ABC的黄金分割线,你认为对吗?说说你的理由;
直线CD是△ABC的黄金分割线,你认为对吗?说说你的理由;(2)请你说明:三角形的中线是否是该三角形的黄金分割线.
分析:(1)结合线段的黄金分割点的概念和三角形的面积公式进行分析计算;
(2)根据三角形的中线的概念可知分成的两个三角形的面积相等,显然不符合黄金分割线的概念.
(2)根据三角形的中线的概念可知分成的两个三角形的面积相等,显然不符合黄金分割线的概念.
解答:解:∵
=
,
=
,
又∵D是AB的黄金分割点,
∴
=
,
=
,
∴CD是△ABC的黄金分割线;
(2)不是.
∵CD是△ABC的中线,
∴AD=DB,
∴
=
,
而
=1,
∴
≠
,
∴中线不是黄金分割线.
| S△ACD |
| S△ABC |
| AD |
| AB |
| S△BCD |
| S△ACD |
| BD |
| AD |
又∵D是AB的黄金分割点,
∴
| AD |
| AB |
| BD |
| AD |
| S△ACD |
| S△ABC |
| S△BCD |
| S△ACD |
∴CD是△ABC的黄金分割线;
(2)不是.
∵CD是△ABC的中线,
∴AD=DB,
∴
| S△ACD |
| S△ABC |
| 1 |
| 2 |
而
| S△BCD |
| s△ACD |
∴
| S△ACD |
| S△ABC |
| S△BCD |
| s△ACD |
∴中线不是黄金分割线.
点评:主要考查的是线段的黄金分割点的概念和三角形的面积公式.

练习册系列答案
相关题目
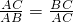 ,那么点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果
,那么点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果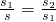 ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.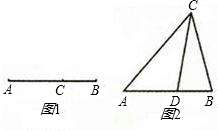 直线CD是△ABC的黄金分割线,你认为对吗?说说你的理由;
直线CD是△ABC的黄金分割线,你认为对吗?说说你的理由; ,那么点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果
,那么点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果 ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.