题目内容
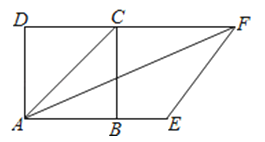
【题目】如图，在矩形ABCD中，过对角线AC的中点O作AC的垂线，分别交射线AD和CB于点E、F，连结AF、CE.
（1）求证：AE=CF.
（2）求证：四边形AFCE是菱形.
【答案】（1）证明见解析；（1）证明见解析.
【解析】试题分析：（1）根据矩形的性质，证明△EOA ≌ △FOC，从而根据全等三角形的性质得证；
（2）根据对角线互相垂直的平行四边形是菱形可得证.
试题解析：（1）∵四边形ABCD是矩形，
∴AE // CF．
∴∠AEO =∠CFO．
∵点O为对角线AC的中点，
∴AO = CO．
又∵∠AOE =∠COF，
∴△EOA ≌ △FOC．
∴AE = CF．
（2）∵AE // CF，AE = CF，
∴四边形AFCE是平行四边形
又∵EF⊥AC，
∴四边形AFCE是菱形
练习册系列答案
世纪百通期末金卷系列答案
相关题目
【题目】思考题：在对某地区的一次人口抽样统计分析中，各年龄段（年龄为整数）的人数如下表所示：
年龄段 | 0～9 | 10～19 | 20～29 | 30～39 | 40～49 | 50～59 | 60～69 | 70～79 | 80～89 |
人数 | 9 | 11 | 17 | 18 | 17 | 12 | 8 | 6 | 2 |
根据此表回答下列问题：
（1）样本中年龄在60岁以上（含60岁）的频率是多少？
（2）如果该地区现有人口80000人，为关注人口老龄化问题，请估算该地区60岁以上（含60岁）的人口数．
【题目】下表记录了某种幼树在一定条件下移植成活情况
移植总数n | 400 | 1500 | 3500 | 7000 | 9000 | 14000 |
成活数m | 325 | 1336 | 3203 | 6335 | 8073 | 12628 |
成活的频率（精确到0.01） | 0.813 | 0.891 | 0.915 | 0.905 | 0.897 | 0.902 |
由此估计这种幼树在此条件下移植成活的概率约是_____（精确到0.1）．
