题目内容
如图①，两个全等的直角三角形的直角顶点及一条直角边重合，∠CAO=30°，OA
=6cm．
（1）求OC的长；
（2）如图②，将△ACB绕点C逆时针旋转30°到△A′CB′的位置，求点A到点A′所经过的路径的长．
解：（1）在Rt△AOC中，
∵∠ACO=90°，∠CAO=30°，OA=6cm，
∴OC=
OA=×6=3（cm）．
（2）在Rt△AOC中，
∵∠ACO=90°，∠CAO=30°，OA=6cm，
∴AC=3
（cm）．
根据题意，得=
（cm）．
分析：（1）利用三角函数值可直接求出OC的长度．
（2）本题只需求出AC的长即可确定旋转半径，从而利用弧长公式即可求出旋转的路径．
点评：本题考查了旋转的性质及弧长的计算，有一定的难度，解答本题的关键是根据题意利用三角形的知识求出线段的长度，然后解题．
∵∠ACO=90°，∠CAO=30°，OA=6cm，
∴OC=
OA=×6=3（cm）．（2）在Rt△AOC中，
∵∠ACO=90°，∠CAO=30°，OA=6cm，
∴AC=3
（cm）．根据题意，得=
（cm）．分析：（1）利用三角函数值可直接求出OC的长度．
（2）本题只需求出AC的长即可确定旋转半径，从而利用弧长公式即可求出旋转的路径．
点评：本题考查了旋转的性质及弧长的计算，有一定的难度，解答本题的关键是根据题意利用三角形的知识求出线段的长度，然后解题．
练习册系列答案
阅读快车系列答案
相关题目
在数学活动课上，老师要求同学们先做下面的“循环分割”操作，然后再探索规律：
如图1，是一等腰梯形纸片，其腰长与上底长相等，且底角分别60°和120°，按要求开始操作（每次分割，纸片均不得留有剩余）；
第1次分割：将原等腰梯形纸片分割成3个等边三角形；
第2次分割：将上次分割出的一个等边三角形分割成3个全等的等腰梯形，然后将刚分割出的一个等腰梯形分割成3个等边三角形；
以后按第2次分割的方法进行下去…请解答下列问题：
（1）请你在图2中画出前两次分割后的图案；
（2）若原等腰梯形的面积为a，请你通过操作、观察，将第2次，第3次分割后所得的一个最小等边三角形的面积分别填入下表：
（3）请你猜想，分割所得的一个最小等边三角形面积S与分割次数n有何关系？（请直接用含a的式子表示，不需写推理过程）
如图1，是一等腰梯形纸片，其腰长与上底长相等，且底角分别60°和120°，按要求开始操作（每次分割，纸片均不得留有剩余）；
第1次分割：将原等腰梯形纸片分割成3个等边三角形；
第2次分割：将上次分割出的一个等边三角形分割成3个全等的等腰梯形，然后将刚分割出的一个等腰梯形分割成3个等边三角形；
以后按第2次分割的方法进行下去…请解答下列问题：
（1）请你在图2中画出前两次分割后的图案；
（2）若原等腰梯形的面积为a，请你通过操作、观察，将第2次，第3次分割后所得的一个最小等边三角形的面积分别填入下表：
| 分割次数（n） | 1 | 2 | 3 | … | ||
| 一个最小等边三角形的面积（S） |
|
… |
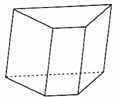27、如图为一直棱柱，其中两底面为全等的梯形，其面积和为16；四个侧面均为长方形，其面积和为45．若此直棱柱的体积为24，则所有边的长度和为（ ）
如图为一直棱柱，其中两底面为全等的梯形，其面积和为16；四个侧面均为长方形，其面积和为45．若此直棱柱的体积为24，则所有边的长度和为在数学活动课上，老师要求同学们先做下面的“循环分割”操作，然后再探索规律：
如图1，是一等腰梯形纸片，其腰长与上底长相等，且底角分别60°和120°，按要求开始操作（每次分割，纸片均不得留有剩余）；
第1次分割：将原等腰梯形纸片分割成3个等边三角形；
第2次分割：将上次分割出的一个等边三角形分割成3个全等的等腰梯形，然后将刚分割出的一个等腰梯形分割成3个等边三角形；
以后按第2次分割的方法进行下去…请解答下列问题：
（1）请你在图2中画出前两次分割后的图案；
（2）若原等腰梯形的面积为a，请你通过操作、观察，将第2次，第3次分割后所得的一个最小等边三角形的面积分别填入下表：
| 分割次数（n） | 1 | 2 | 3 | … |
| 一个最小等边三角形的面积（S） |  a | … |
