题目内容
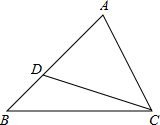（2012•长春）如图，在△ABC中，AB=5，AC=4，点D在边AB上，∠ACD=∠B，则AD的长为| 16 |
| 5 |
| 16 |
| 5 |
分析：先根据相似三角形的判定定理得出△ACD∽△ABC，再由相似三角形的对应边成比例即可得出AD的长．
解答：解：∵在△ABC与△ACD中，∠A=∠A，∠ACD=∠B，
∴△ACD∽△ABC，
∴
=
，
∵AB=5，AC=4，
∴
=
，
解得AD=
．
故答案为：
．
∴△ACD∽△ABC，
∴
| AC |
| AB |
| AD |
| AC |
∵AB=5，AC=4，
∴
| 4 |
| 5 |
| AD |
| 4 |
解得AD=
| 16 |
| 5 |
故答案为：
| 16 |
| 5 |
点评：本题考查的是相似三角形的判定与性质，根据题意判断出△ACD∽△ABC是解答此题的关键．
练习册系列答案
相关题目
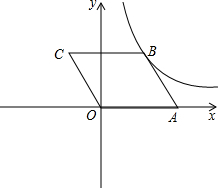（2012•长春）如图，在平面直角坐标系中，?OABC的顶点A、C的坐标分别为A（2，0）、C（-1，2），反比例函数y=
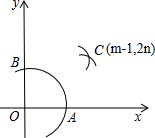（2012•长春）如图，在平面直角坐标系中，在x轴、y轴的正半轴上分别截取OA、OB，使OA=OB；再分别以点A、B为圆心，以大于
（2012•长春）如图是2012年伦敦奥运会吉祥物，某校在五个班级中对认识它的人数进行了调查，结果为（单位：人）：30，31，27，26，31．这组数据的中位数是（ ）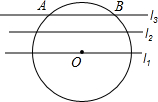
（2012•长春）如图，在同一平面内，有一组平行线l1、l2、l3，相邻两条平行线之间的距离均为4，点O在直线l1上，⊙O与直线l3的交点为A、B，AB=12，求⊙O的半径．