Question

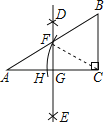
【题目】如图，AB是半圆O的直径，C是半圆上一个动点（不与点A，B重合），D是弦AC上一点，过点D作DE⊥AB，垂足为E，过点C作半圆O的切线，交ED的延长线于点F．

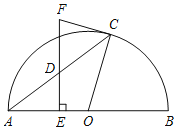
（1）求证：FC＝FD．

（2）①当∠CAB的度数为　 　时，四边形OEFC是矩形；②若D是弦AC的中点，⊙O的半径为5，AC＝8，则FC的长为　 　．

Answer 1

【答案】（1）见解析；（2）①45；② .

【解析】

(1)证明∠FDC＝∠FCD，即可求解；

(2)①当∠CAB＝45°时，∠COB＝90°，即可求解；

②连接OD，过点F作FM⊥CD，垂足为M，设∠FDC＝α，由D是弦AC的中点，则OD⊥AC，求出cosα＝，继而根据FD＝即可求解．

(1)∵FC是圆的切线，

∴∠FCD+∠ACO＝90°，

∵FE⊥BA，∴∠ADC+∠CAO＝90°，

而∠CAO＝∠ACO，∠ADE＝∠FDC，

∴∠FDC＝∠FCD，

∴FC＝FD；

(2)①当∠CAB＝45°时，∠COB＝90°，

则四边形OEFC是矩形，

故答案为:45；

②连接OD，过点F作FM⊥CD，垂足为M，

设∠FDC＝α，

∵ FD=FC，∴DM=CD，

∵D是弦AC的中点，

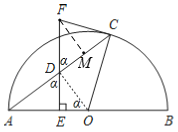
∴OD⊥AC，AD＝DC，

∴∠ADE+∠EDO=90°，

∵∠DEO=90°，

∴∠EDO+∠EOD=90°，

∴∠ADE＝∠AOD＝∠FDC＝α，

∵AD＝CD＝AC＝4，OA＝5，

∴DO＝=3，

∴cosα＝，

∴在△FDC中，FD＝＝，

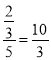∴FC=．