题目内容
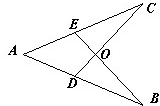 13、如图,已知点D,E分别在线段AB,AC上,BE,CD相交于点O,且AE=AD,添加以下四个条件中的一个,其中不能使△ABE≌△ACD的条件是( )
13、如图,已知点D,E分别在线段AB,AC上,BE,CD相交于点O,且AE=AD,添加以下四个条件中的一个,其中不能使△ABE≌△ACD的条件是( )分析:三角形全等条件中必须是三个元素,并且一定有一组对应边相等.在△ABE和△ACD中,已知了AE=AD,公共角∠A,因此只需添加一组对应角相等或AC=AB即可判定两三角形全等.
解答:解:已知了AE=AD,公共角∠A,
A、如添加AB=AC,利用SAS即可证明△ABE≌△ACD;
B、如添加∠ADC=∠AEB,利用ASA即可证明△ABE≌△ACD;
C、如添加BE=CD,因为SSA,不能证明△ABE≌△ACD,所以此选项不能作为添加的条件;
D、如添∠C=∠B利用AAS即可证明△ABE≌△ACD.
故选C.
A、如添加AB=AC,利用SAS即可证明△ABE≌△ACD;
B、如添加∠ADC=∠AEB,利用ASA即可证明△ABE≌△ACD;
C、如添加BE=CD,因为SSA,不能证明△ABE≌△ACD,所以此选项不能作为添加的条件;
D、如添∠C=∠B利用AAS即可证明△ABE≌△ACD.
故选C.
点评:此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加时注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
 18、如图,已知点M、N分别是△ABC的边BC、AC的中点,点P是点A关于点M的对称点,点Q是点B关于点N的对称点,求证:P、C、Q三点在同一条直线上.
18、如图,已知点M、N分别是△ABC的边BC、AC的中点,点P是点A关于点M的对称点,点Q是点B关于点N的对称点,求证:P、C、Q三点在同一条直线上. 如图,已知点M、N分别是平行四边形ABCD的边AB、DC的中点,求证:∠DAN=∠BCM.
如图,已知点M、N分别是平行四边形ABCD的边AB、DC的中点,求证:∠DAN=∠BCM. 21、如图,已知点E、F分别是菱形ABCD的边AB、AD上,BE=DF,
21、如图,已知点E、F分别是菱形ABCD的边AB、AD上,BE=DF, (2013•金山区二模)如图,已知点D,E分别是边AC和AB的中点,设
(2013•金山区二模)如图,已知点D,E分别是边AC和AB的中点,设 如图,已知点E、F分别是AC、AB的中点,其中△AFE的面积为2,则△EFG的面积为
如图,已知点E、F分别是AC、AB的中点,其中△AFE的面积为2,则△EFG的面积为