题目内容
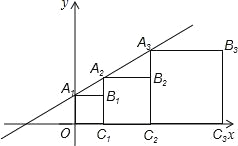
【题目】在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).
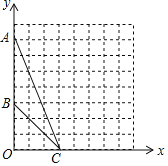
(1)在图中作出△ABC的外接圆⊙P(保留必要的作图痕迹,不写作法)
(2) 若在x轴的正半轴上有一点D(异与C点),且∠ADB=∠ACB,则点D的坐标为 .
(3)若用扇形PAC围成一个圆锥,那么这个圆锥的底面半径为 .
【答案】(1)如图所示即为△ABC的外接圆⊙P;见解析;(2)(7,0);(3)![]() .
.
【解析】
(1)三角形外接圆的圆心即为三边垂直平分线的交点,找出AB与BC的交点即为圆心;
(2)根据条件可得点D在⊙P上,即圆与x轴的交点,根据图形即可得D点坐标;
(3)根据圆锥底面圆的周长=扇形弧长求解.
解:(1)AB和BC的垂直平分线的交点即为△ABC的外接圆的圆心P,
以P为圆心,PA为半径作⊙P.
如图所示即为△ABC的外接圆⊙P;
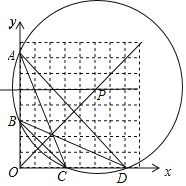
(2)∵∠ADB=∠ACB,
∴D点在⊙P上,点D为圆与x轴的交点,
如图所示:点D的坐标为(7,0);
故答案为:(7,0).
(3)设底面圆半径为r,圆锥母线长为l,
圆锥底面圆的周长=扇形弧长,
即2πr=![]()
∵PA=![]() =
=![]() ,
,
∴r=![]() .
.
故答案为![]() .
.

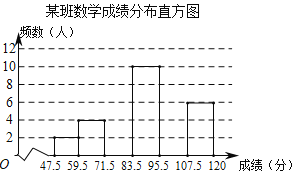
【题目】某市为了解九年级学生数学模拟考试成绩情况,随机抽取部分学生的成绩进行分析,制成频数分布表如下(成绩得分均为整数):
组别 | 成绩分组 | 频数 | 频率 |
1 | 47.5~59.5 | 2 | 0.05 |
2 | 59.5~71.5 | 4 | 0.10 |
3 | 71.5~83.5 | a | 0.2 |
4 | 83.5~95.5 | 10 | 0.25 |
5 | 95.5~107.5 | b | c |
6 | 107.5~120 | 6 | 0.15 |
合计 | d | 1.00 |
根据表中提供的信息解答下列问题:
(1)频数分布表中的a= ,b= ,c= ,d= ;
(2)补充完整频数分布直方图.
(3)已知全市九年级共有3500名学生参加考试,成绩96分及以上为优秀,估计全市九年级学生数学模拟考试成绩为优秀的学生人数是多少?