题目内容
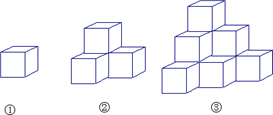
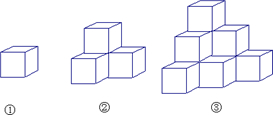
下列各图是棱长为1cm的小正方体摆成的,如图①中,共有1个小正方体,从正面看有1个正方形,表面积为6cm2;如图②中,共有4个小正方体,从正面看有3个正方形,表面积为18cm2;如图③,共有10个小正方体,从正面看有6个正方形,表面积为36cm2;…(1)第6个图中,共有多少个小正方体?从正面看有多少个正方形?表面积是多少?
(2)第n个图形中,从正面看有多少个正方形?表面积是多少?
分析:(1)由题意知,第4个图共有1+3+6+10=20个,从正面看有10个正方形,第5个图共有1+3+6+10+15=35个,从正面看有15个正方形,即可推出第6个图形的正方体和正面看到的正方形个数;
(2)由题意知,从正面看有(1+2+3+4+…+n)个正方形,即可得出其表面积;
(2)由题意知,从正面看有(1+2+3+4+…+n)个正方形,即可得出其表面积;
解答:解:(1)由题意可知,第6个图中,共有1+3+6+10+15+21=56个正方体,
从正面看有1+2+3+4+5+6=21个正方形,表面积为:21×6=126cm2;
(2)由题意知,从正面看到的正方形个数有(1+2+3+4+…+n)=
个,
表面积为:
×6=
=3n(n+1)cm2.
从正面看有1+2+3+4+5+6=21个正方形,表面积为:21×6=126cm2;
(2)由题意知,从正面看到的正方形个数有(1+2+3+4+…+n)=
| (n+1)n |
| 2 |
表面积为:
| (n+1)n |
| 2 |
| 6n(n+1) |
| 2 |
点评:本题主要考查了平面图形的有规律变化,要求学生通过观察图形,分析、归纳发现其中的规律,并应用规律解决问题.

练习册系列答案
相关题目
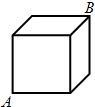 如图是棱长为4cm的立方体木块,一只蚂蚁现在A点,若在B点处有一块糖,它想尽快吃到这块糖,则蚂蚁沿正方体表面爬行的最短路程是
如图是棱长为4cm的立方体木块,一只蚂蚁现在A点,若在B点处有一块糖,它想尽快吃到这块糖,则蚂蚁沿正方体表面爬行的最短路程是

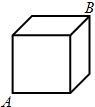 如图是棱长为4cm的立方体木块,一只蚂蚁现在A点,若在B点处有一块糖,它想尽快吃到这块糖,则蚂蚁沿正方体表面爬行的最短路程是________cm.
如图是棱长为4cm的立方体木块,一只蚂蚁现在A点,若在B点处有一块糖,它想尽快吃到这块糖,则蚂蚁沿正方体表面爬行的最短路程是________cm.