题目内容
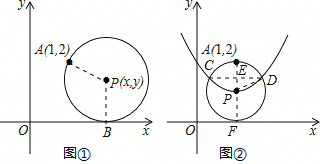
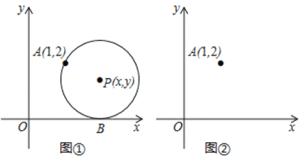
【题目】如图,在平面直角坐标系中,圆心为P(![]() ,
,![]() )的动圆经过点A(1,2)且与
)的动圆经过点A(1,2)且与![]() 轴相切于点B.
轴相切于点B.
(1)当![]() =2是,求⊙P的半径;
=2是,求⊙P的半径;
(2)求![]() 关于
关于![]() 的函数解析式,在图②中画出此函数图像;
的函数解析式,在图②中画出此函数图像;
(3)请类比圆的定义(圆可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图像进行定义:此函数图像可以看成是到 的距离等于到 的距离的所有点的集合;
(4)当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(![]() ,
,![]() )在点C的右侧,请利用图②,则cos∠APD= .
)在点C的右侧,请利用图②,则cos∠APD= .
【答案】(1)圆P的半径为1.25 ;(2)y= (x﹣1)2+1,图象详见解析;(3)点A, x轴;(4)cos∠APD= = ﹣2+![]() .
.
【解析】
(1)根据两点间距离公式列式计算即可;
(2)同(1)列出式子并整理,可得y=(x﹣1)2+1,然后描点画图即可;
(3)由(x﹣1)2+(y﹣2)2=y2可知此函数图像可以看成是到点A的距离等于到x轴的距离的所有点的集合;
(4)连接CD,连接AP并延长,交x轴于点F,设PE=a,用a表示出D点坐标,代入到抛物线解析式求出a的值,
解:(1)由x=2,得到P(2,y),
连接AP,PB,
∵圆P与x轴相切,
∴PB⊥x轴,即PB=y,
由AP=PB,得到![]() ,
,
解得:y=1.25 ,则圆P的半径为1.25 ;
(2)同(1),由AP=PB,得到(x﹣1)2+(y﹣2)2=y2,
整理得:y= (x﹣1)2+1,即图象为开口向上的抛物线,
画出函数图象,如图②所示;
(3)由(x﹣1)2+(y﹣2)2=y2可知此函数图像可以看成是到点A的距离等于到x轴的距离的所有点的集合;
(4)连接CD,连接AP并延长,交x轴于点F,
设PE=a,则有EF=a+1,ED=![]() ,
,
∴D坐标为(![]() ,a+1),
,a+1),
代入抛物线解析式得:a+1= 0.25(1﹣a2)+1,
解得:a=﹣2+![]() 或a=﹣2﹣
或a=﹣2﹣![]() (舍去),即PE=﹣2+
(舍去),即PE=﹣2+![]() ,
,
在Rt△PED中,PE=﹣2+![]() ,PD=1,
,PD=1,
则cos∠APD=﹣2+![]() .
.