题目内容
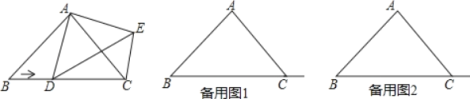
【题目】如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.

(1)求证:△ABC≌△DCB;
(2)过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N,试判断△BNC的形状,并证明你的结论.
【答案】(1)见解析;(2)△BNC是等腰三角形,证明见解析
【解析】
(1)由SSS可证△ABC≌△DCB;
(2)△BNC是等腰三角形,可先证明四边形BMCN是平行四边形,由(1)知,∠MBC=∠MCB,可得BM=CM,于是就有四边形BMCN是菱形,则BN=CN.
(1)证明:如图,在△ABC和△DCB中,
∵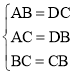 ,
,
∴△ABC≌△DCB(SSS);
(2)解:△BNC是等腰三角形.证明如下:
∵CN∥BD,BN∥AC,
∴四边形BMCN是平行四边形,
由(1)知,∠MBC=∠MCB,
∴BM=CM(等角对等边),
∴四边形BMCN是菱形,
∴BN=CN.∴△BNC是等腰三角形

练习册系列答案
相关题目