题目内容
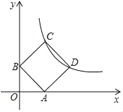
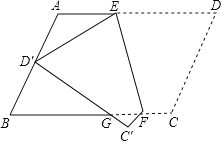
【题目】如图,在平行四边形ABCD中,AB=![]() ,BC=8,∠B=60°,将平行四边形ABCD沿EF折叠,点D恰好落在边AB的中点D′处,折叠后点C的对应点为C′,D′C′交BC于点G,∠BGD′=32°.
,BC=8,∠B=60°,将平行四边形ABCD沿EF折叠,点D恰好落在边AB的中点D′处,折叠后点C的对应点为C′,D′C′交BC于点G,∠BGD′=32°.
(1)求∠D′EF的度数;
(2)求线段AE的长.
【答案】(1)∠D'EF=76°;(2)![]() .
.
【解析】
(1)根据折叠的性质可得:∠D=∠ED'G=60°,∠DEF=∠D'EF,根据平行线的性质有∠DEF=∠EFB.等量代换得到∠D'EF=∠EFB,在四边形![]() 中,根据四边形的内角和即可求解.
中,根据四边形的内角和即可求解.
(2)过点E作EH⊥AB于点H,设AE=x,根据平行线的性质有∠HAD=∠B=60°,且EH⊥AB,求出![]() 根据中点的性质有
根据中点的性质有![]() 根据勾股定理即可求解.
根据勾股定理即可求解.
解:(1)∵四边形ABCD是平行四边形,
∴∠B=∠D=60°,AD∥BC,
∴∠DEF=∠EFB.
∵将平行四边形ABCD沿EF折叠,点D恰好落在边AB的中点D′处,
∴∠D=∠ED'G=60°,∠DEF=∠D'EF,
∴∠D'EF=∠EFB,
∵∠BGD′=32°
∴∠D'GF=148°
∵∠D'GF+∠EFB+∠D'EF+∠ED'G=360°,
![]() ,
,
∴∠D'EF=76°;
(2)过点E作EH⊥AB于点H,
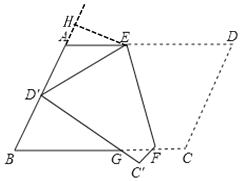
设AE=x,
∵AD∥BC,
∴∠HAD=∠B=60°,且EH⊥AB,
∴![]()
∵点D'是AB中点,
∴![]()
∵HE2+D'H2=D'E2,
∴![]()
∴x=![]() ,
,
∴![]() .
.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目