题目内容
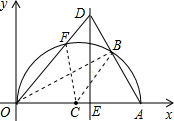
如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上的一动点，连接AB，并延长AB至点D，使DB=AB，连接OD交半圆C于点F，过点D作x轴垂线，分别交x轴于点E，点E为垂足．当∠AOF=60°时，弧BF的度数是______；当DE=8时，线段AE的长是______．
连接OB，FC，BC
∵OA是⊙C直径，∴∠OBA=90°，
又∵AB=BD，
∴OB是AD的垂直平分线，
∴OD=OA=10，
∴∠BOA=∠DOB=30°，
∴∠BCA=∠FCB=60°，
∴弧BF的度数是60°，
在Rt△ODE中，
OE=
=
=6，
∴AE=AO-OE=10-6=4，
故答案为：60°，4．
∵OA是⊙C直径，∴∠OBA=90°，
又∵AB=BD，
∴OB是AD的垂直平分线，
∴OD=OA=10，
∴∠BOA=∠DOB=30°，
∴∠BCA=∠FCB=60°，
∴弧BF的度数是60°，
在Rt△ODE中，
OE=
| OD2-DE2 |
| 102-82 |
∴AE=AO-OE=10-6=4，
故答案为：60°，4．
练习册系列答案
相关题目
选用适当的数，设计出计算半圆O的半径r的一种方案：
别交PC，CB于点D，F．