题目内容
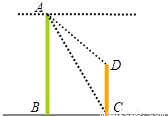
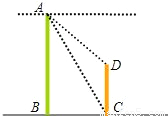
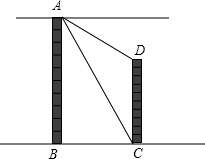 如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为多少米?
如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为多少米?
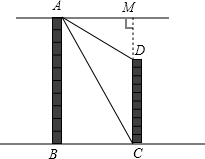 解:延长CD交AM于点M,则AM=30.
解:延长CD交AM于点M,则AM=30.∴DM=AM×tan30°=10
 .
.同理可得CM=30
 .
.∴CD=CM-DM=20
 (米).
(米).答:建筑物CD的高为20
 米.
米.分析:延长CD交AM于点M.在Rt△ACM中,可求出CM;在Rt△ADM中,可求出DM.CD=CM-DM.
点评:考查解直角三角形的应用;得到以AM为公共边的2个直角三角形是解决本题的突破点.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
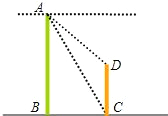 如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为
如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为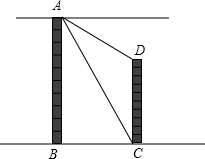 如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为多少米?
如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为多少米?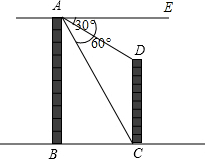 如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°.求建筑物CD的高(
如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°.求建筑物CD的高(