题目内容
如图,在直角坐标系中,点A,B,C的坐标分别为(-1,0),(3,0),(0,3),过A,B,C三点的抛物的对称轴为直线l,D为对称轴l上一动点.(1)求抛物线的解析式;
(2)求当AD+CD最小时点D的坐标;
(3)以点A为圆心,以AD为半径作⊙A.
①证明:当AD+CD最小时,直线BD与⊙A相切;
②写出直线BD与⊙A相切时,D点的另一个坐标:______.

【答案】分析:(1)由待定系数法可求得抛物线的解析式.
(2)连接BC,交直线l于点D,根据抛物线对称轴的性质,点B与点A关于直线l对称,∴AD=BD.
∴AD+CD=BD+CD,由“两点之间,线段最短”的原理可知:D在直线BC上AD+CD最短,所以D是直线l与直线BC的交点,
设出直线BC的解析式为y=kx+b,可用待定系数法求得BC直线的解析式,故可求得BC与直线l的交点D的坐标.
(3)由(2)可知,当AD+CD最短时,D在直线BC上,由于已知A,B,C,D四点坐标,根据线段之间的长度,可以求出△ABD是直角三角形,即BC与圆相切.由于AB⊥l,故由垂径定理知及切线长定理知,另一点D与现在的点D关于x轴对称,所以另一点D的坐标为(1,-2).
解答:解:
(1)设抛物线的解析式为y=a(x+1)(x-3).(1分)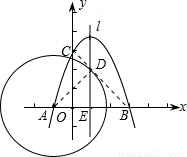
将(0,3)代入上式,得3=a(0+1)(0-3).
解,得a=-1.(2分)∴抛物线的解析式为y=-(x+1)(x-3).
即y=-x2+2x+3.(3分)
(2)连接BC,交直线l于点D.
∵点B与点A关于直线l对称,
∴AD=BD.(4分)
∴AD+CD=BD+CD=BC.
由“两点之间,线段最短”的原理可知:
此时AD+CD最小,点D的位置即为所求.(5分)
设直线BC的解析式为y=kx+b,
由直线BC过点(3,0),(0,3),
得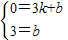
解这个方程组,得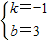
∴直线BC的解析式为y=-x+3.(6分)
由(1)知:对称轴l为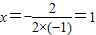 ,即x=1.
,即x=1.
将x=1代入y=-x+3,得y=-1+3=2.
∴点D的坐标为(1,2).(7分)
说明:用相似三角形或三角函数求点D的坐标也可,答案正确给(2分).
(3)①连接AD.设直线l与x轴的交点记为点E.
由(2)知:当AD+CD最小时,点D的坐标为(1,2).
∴DE=AE=BE=2.
∴∠DAB=∠DBA=45度.(8分)
∴∠ADB=90度.
∴AD⊥BD.
∴BD与⊙A相切.(9分)
②∵另一点D与D(1,2)关于x轴对称,
∴D(1,-2).(11分)
点评:本题考查抛物线与数轴交点问题,以及顶点坐标公式,顶点与对称轴之间的关系,圆与直线相切时的性质,两点之间线段最短,垂径定理和切线长定理等定理.
(2)连接BC,交直线l于点D,根据抛物线对称轴的性质,点B与点A关于直线l对称,∴AD=BD.
∴AD+CD=BD+CD,由“两点之间,线段最短”的原理可知:D在直线BC上AD+CD最短,所以D是直线l与直线BC的交点,
设出直线BC的解析式为y=kx+b,可用待定系数法求得BC直线的解析式,故可求得BC与直线l的交点D的坐标.
(3)由(2)可知,当AD+CD最短时,D在直线BC上,由于已知A,B,C,D四点坐标,根据线段之间的长度,可以求出△ABD是直角三角形,即BC与圆相切.由于AB⊥l,故由垂径定理知及切线长定理知,另一点D与现在的点D关于x轴对称,所以另一点D的坐标为(1,-2).
解答:解:
(1)设抛物线的解析式为y=a(x+1)(x-3).(1分)
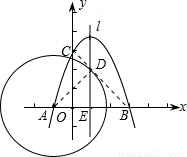
将(0,3)代入上式,得3=a(0+1)(0-3).
解,得a=-1.(2分)∴抛物线的解析式为y=-(x+1)(x-3).
即y=-x2+2x+3.(3分)
(2)连接BC,交直线l于点D.
∵点B与点A关于直线l对称,
∴AD=BD.(4分)
∴AD+CD=BD+CD=BC.
由“两点之间,线段最短”的原理可知:
此时AD+CD最小,点D的位置即为所求.(5分)
设直线BC的解析式为y=kx+b,
由直线BC过点(3,0),(0,3),
得
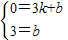
解这个方程组,得
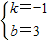
∴直线BC的解析式为y=-x+3.(6分)
由(1)知:对称轴l为
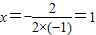 ,即x=1.
,即x=1.将x=1代入y=-x+3,得y=-1+3=2.
∴点D的坐标为(1,2).(7分)
说明:用相似三角形或三角函数求点D的坐标也可,答案正确给(2分).
(3)①连接AD.设直线l与x轴的交点记为点E.
由(2)知:当AD+CD最小时,点D的坐标为(1,2).
∴DE=AE=BE=2.
∴∠DAB=∠DBA=45度.(8分)
∴∠ADB=90度.
∴AD⊥BD.
∴BD与⊙A相切.(9分)
②∵另一点D与D(1,2)关于x轴对称,
∴D(1,-2).(11分)
点评:本题考查抛物线与数轴交点问题,以及顶点坐标公式,顶点与对称轴之间的关系,圆与直线相切时的性质,两点之间线段最短,垂径定理和切线长定理等定理.

练习册系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: